Question

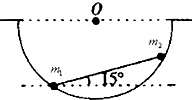如图所示，一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面是光滑的．一根质量可忽略的刚性细杆两端分别固定着质量为m₁和m₂的小球，放置在半球面内．已知细杆长度是球面半径的

2

倍，当两球处于平衡状态时，细杆与水平面的夹角θ=15°，则两小球的质量比m₂/m₁为（　　）

• A、

  3

  ：2
• B、2：

  3

• C、

  3

  ：1
• D、1：

  3

Answer 1

分析：本题可以以O点为支点，根据力矩平衡条件列式，求解两球质量之比，要抓住半球形的碗对两球的支持力指向球心，力臂为零，力矩为零．

解答：解：设半球形的碗半径为R，已知细杆长度是球面半径的

2

倍，根据几何知识得，Om₁与杆间的夹角为45°，Om₁与水平方向的夹角为60°，Om₂与竖直方向的夹角为60°，则以O点为支点，根据力矩平衡条件得：
   m₁gRcos60°=m₂gRsin60°
则得

m2

m1

=

1

3

故选D

点评：本题根据力矩平衡条件，回避了支持力的作用，解答比较简单，也可以根据共点力平衡求解，但比较麻烦．