题目内容
【题目】如图所示，一个半径为R的绝缘光滑圆轨道固定在竖直面内，A、B和C、D分别是圆轨道水平直径和竖直直径的两个端点，O点是圆心。一个质量为m、带电荷量为+q的小球(可视为质点)放在圆轨道的最低点C。在水平直径AB的下方存在匀强电场，电场方向平行于轨道所在的平面且水平向右，电场强度为E=
(g为重力加速度)。下列说法正确的是（ ）
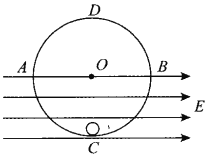
A. 在C点由静止释放小球，小球会在C点和B点之间做往复运动
B. 若小球从C点以大小为
的速度向右运动，则小球刚好能够通过D点
C. 若在C点给小球水平向右的初速度，使小球能够通过D点，则小球每次经过D点时对轨道的作用力都会比前一次通过D点时大4mg
D. 若小球刚好能够向左通过D点，则到A点时由于受到水平方向的电场力作用，小球会脱离轨道
【答案】AC
【解析】
（1）从C点由静止释放小球后，对其进行受力分析，确定其处于自然静止状态（平衡位置）时所处的位置，根据运动的对称性，可解决A项；
（2）根据竖直平面圆周运动最高点轻绳模型的临界条件，可计算小球刚好通过D点时的临界最小速度，然后从C到D利用动能定理，即可判断B项；
（3）若小球能通过D点，则D点既是研究的起点也是终点，利用动能定理，结合牛顿第二定理即可求解C项；
（4）根据圆周运动的临界条件，可判断D。
A、若小球C在电场和重力场的复合场中处于自然平衡状态时，对其进行受力分析，如图所示，
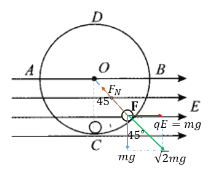
小球的平衡位置与球心的连线，与竖直方向的夹角为45度，C和B关于连线对称。根据受力的对称性可知，当小球从C点被由静止释放后，将在C点和B点之间做往复运动，A正确；
B、若小球恰好通过D点，则在D点只有重力提供向心力，
；设小球在C点以
开始向右运动，恰好通过最高点D，则根据动能定理有：
，解得
，故B错误；
C、设某次小球向左通过D点的速度为
，轨道对其弹力大小为N，则根据牛顿第二定律可知：
，当以D为起点，小球逆时针再次回到D点的过程中，根据动能定理得：
，此时小球经过D点，轨道对其弹力大小为
，满足
，联立接得
，故C正确；
D、若小球恰好向左通过D点，则此时重力mg提供向心力，从D到A，小球速度会增加，所以到达A点时，小球需要的向心力会大于mg，即需要的向心力大于qE，所以小球在A点必然和轨道之间有弹力作用，小球在A点不会脱离轨道，D错误。
故本题选AC。
