Question

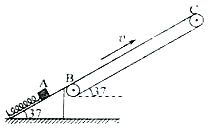
【题目】如图所示，一质量m=1kg的小物块（可视为质点），放置在质量M=4kg的长木板左侧，长木板放置在光滑的水平面上。初始时，长木板与物块一起以水平速度向左匀速运动。在长木板的左侧上方固定着一障碍物A，当物块运动到障碍物A处时与A发生弹性碰撞（碰撞时间极短，无机械能损失），而长木板可继续向左运动。重力加速度g取10m/s2。

（1）设长木板足够长，求物块与障碍物第一次碰撞后，物块与长木板速度相同时的共同速率；

（2）设长木板足够长，物块与障碍物第一次碰撞后，物块向右运动能达到的最大距离是s=0.4m，求物块与长木板间的动摩擦因数以及此过程中长木板运动的加速度的大小；

（3）要使物块不会从长木板上滑落，长木板至少为多长？

Answer 1

【答案】（1）l. 2m/s （2） （3）2m

【解析】

（1）物块与固定障碍物碰撞时无机械能损失，所以碰后反向弹回，速度大小为v0，物块与木板组成的系统合力为0，遵守动量守恒定律，取向左的方向为正方向。

解得v=l. 2m/s

（2）物块与障碍物第一次碰撞后向右做减速运动，速度减为零时右运动的距离最大。

由动能定理得

解得。

对木板由牛顿第二定律得

解得。

（3）只有物块和木板的速度都为0时，物块才不再与障碍物碰撞，即最终物块与木板同时静止，设物块相对木板滑动的相对位移为l，则由能量守恒定律得

解得，

可知木板的长度至少为2m。