��Ŀ����
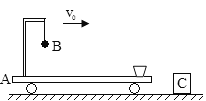
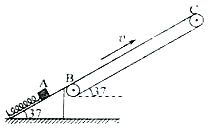
����Ŀ�����õ��ɵ���ʹ��ʹ����Խ������������ߴ�����ͼ��ʾ�����ʹ���ˮƽ�����37�Ƚǣ�˳ʱ�������˶����ٶ�v��4m/s��B��C�ֱ��Ǵ��ʹ������ֵ��е㣬���L��6.4m�����Ҳ��![]() ��б��̶��ڵ������봫�ʹ��ϵ�B�����öԽӡ�һԭ��С��б�泤���ᵯ��ƽ��б����ã��¶˹̶���б��ˣ��϶˷�һ����m��1kg�Ĺ���������Ϊ�ʵ㣩������������ѹ����A����ɾ�ֹ�ͷţ������뿪б�涥�˻���B��ʱ�ٶ�v0��8m/s��A��B��ľ���x��1m��������б�桢���ʹ��ʵĶ�Ħ��������ͬ����Ϊ����0.5����������C�㼴Ϊ�����̽�����gȡ10m/s2��sin37�㣽0.6��cos37�㣽0.8����
��б��̶��ڵ������봫�ʹ��ϵ�B�����öԽӡ�һԭ��С��б�泤���ᵯ��ƽ��б����ã��¶˹̶���б��ˣ��϶˷�һ����m��1kg�Ĺ���������Ϊ�ʵ㣩������������ѹ����A����ɾ�ֹ�ͷţ������뿪б�涥�˻���B��ʱ�ٶ�v0��8m/s��A��B��ľ���x��1m��������б�桢���ʹ��ʵĶ�Ħ��������ͬ����Ϊ����0.5����������C�㼴Ϊ�����̽�����gȡ10m/s2��sin37�㣽0.6��cos37�㣽0.8����
��1������ѹ����A��ʱ�ĵ������ܣ�
��2�������ش��ʹ���B���ϻ���C�����õ�ʱ�䣻
��3�������ش��ʹ���B���ϻ���C��Ĺ����У������ʹ��ʹ�������Ħ����������������
���𰸡�(1)42J,(2)2.4s,(3)19.2J
��������
��1���������غ㶨�ɵã����ɵ����������Ϊ��
![]()
��ã�Ep��42J
��2�������ڼ��ٵ��봫�ʹ��ٶ���ȵĹ����У����ٶ�Ϊa1����ţ�ٵڶ����ɵã�
![]()
��ã�a1��10m/s2
�����봫�ʹ�������Ҫʱ��Ϊ��![]()
��ã�t1��0.4s
��������λ�ƴ�СΪ��![]()
��ã�![]()
��Ϊ![]() �����Թ������ش��ʹ����������ϻ����ڼ����ϻ������м��ٶ�Ϊa2�����У�
�����Թ������ش��ʹ����������ϻ����ڼ����ϻ������м��ٶ�Ϊa2�����У�
![]()
��ã�a2��2m/s2
���蹤���ٶȼ�Ϊ0ʱ������δ�Ӵ��ʹ��ϻ��䣬���˶�ʱ��Ϊ��
![]()
��ã�t2��2s
��������λ�ƴ�СΪ��![]()
��ã�x2��4m
�����˶���C��ʱ�ٶ�ǡ��Ϊ�㣬�ʼ��������
�����ڴ��ʹ����ϻ�����ʱ��Ϊ��t��t1+t2��2.4s
��3����һ�Σ���������λ��Ϊ��x1��2.4m��
���ʹ�λ��![]() �����λ��Ϊ��
��������![]() ��
��
Ħ������Ϊ��![]()
��ã�Q1��3.2J
�ڶ��Σ���������λ��Ϊ��x2��4m��
���ʹ�λ��Ϊ��![]()
������![]()
Ħ������Ϊ�� ![]()
��ã�Q2��16J
��������Q��19.2J��