Question

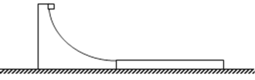
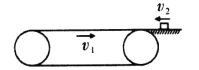
【题目】如图所示，一长的水平传送带以的恒定速率沿顺时针方向转动，传送带右端有一与传送带等高的光滑水平面，一质量的物块以的速率沿直线向左滑上传送带，经过一段时间后物块离开了传送带，已知物块与传送带间的动摩擦因数，重力加速度g取，则以下判断正确的是（　　）

A.经过后物块从传送带的左端离开传送带

B.经过后物块从传送带的右端离开传送带

C.在t时间内传送带对物块做的功为-4J

D.在t时间内由于物块与传送带间摩擦而产生的热量为16J

Answer 1

【答案】BD

【解析】

AB．当物块滑上传送带后，受到传送带向右的摩擦力，根据牛顿第二定律有

代入数据可得物块加速度大小a=1m/s2，方向向右，设物块速度减为零的时间为t1，则有

代入数据解得t1=1s；物块向左运动的位移有

代入数据解得

故物块没有从传送带左端离开；当物块速度减为0后向右加速，根据运动的对称性可知再经过1s从右端离开传送带，离开时速度为1m/s，在传送带上运动的时间为

t=2t1=2s

故A错误，B正确；

C．在t=2s时间内，物块速度大小不变，即动能没有改变，根据动能定理可知传送带对物块做的功为0，故C错误；

D．由前面分析可知物块在传送带上向左运动时，传送带的位移为

当物块在传送带上向右运动时，时间相同传送带的位移也等于x1，故整个过程传送带与物块间的相对位移为

在t时间内由于物块与传送带间摩擦而产生的热量为

故D正确。

故选BD。