题目内容
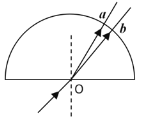
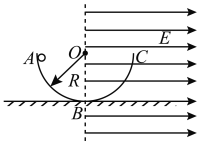
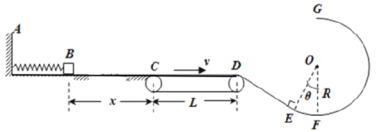
【题目】如图甲所示,在边界为![]() 的竖直狭长区域内存在垂直纸面向里的匀强磁场,磁感应强度
的竖直狭长区域内存在垂直纸面向里的匀强磁场,磁感应强度![]() ,在L1的左侧充满斜向上与水平方向夹角为
,在L1的左侧充满斜向上与水平方向夹角为![]() 的匀强电场
的匀强电场![]() (
(![]() 大小未知)。一带正电的微粒从a点由静止释放,微粒沿水平直线运动到
大小未知)。一带正电的微粒从a点由静止释放,微粒沿水平直线运动到![]() 边界上的b点,这时开始在
边界上的b点,这时开始在![]() 之间的区域内加一竖直方向周期性变化的匀强电场
之间的区域内加一竖直方向周期性变化的匀强电场![]() ,
,![]() 随时间变化的图像如图乙所示(
随时间变化的图像如图乙所示(![]() 表示电场方向竖直向上),微粒从b点沿水平直线运动到c点后,做一次完整的圆周运动,再沿水平直线运动到
表示电场方向竖直向上),微粒从b点沿水平直线运动到c点后,做一次完整的圆周运动,再沿水平直线运动到![]() 边界上的d点。已知c点为线段bd的中点,重力加速度
边界上的d点。已知c点为线段bd的中点,重力加速度![]() 。求:
。求:
(1)微粒的比荷![]() ;
;
(2)a点到b点的距离;
(3)将边界![]() 左右移动以改变正交场的宽度,使微粒仍能按上述运动过程通过相应的区域,求电场
左右移动以改变正交场的宽度,使微粒仍能按上述运动过程通过相应的区域,求电场![]() 变化周期T的最小值。
变化周期T的最小值。

【答案】(1)![]() ;(2)0.2m;(3)0.728s
;(2)0.2m;(3)0.728s
【解析】
(1)由微粒运动到c点后做一次完整的圆周运动可知
![]()
解得
![]()
(2)分析可知微粒从b到c和从c到d均做匀速直线运动,设速度为v,则由受力分析及平衡条件得
![]()
代入数据结合(1)的分析解得
![]()
由题意分析可知,微粒从a到b做匀加速直线运动,合力一定由a指向b,受力分析如图甲所示
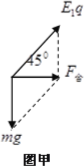
根据几何关系可知
![]()
故微粒从a到b过程中由动能定理得
![]()
代入数据解得
![]()
(3)微粒在正交场中做匀速圆周运动,可得
![]()
结合前面分析代入数据解得轨道半径![]() ;微粒做匀速圆周运动的周期
;微粒做匀速圆周运动的周期
![]()
由于R和![]() 均恒定不变,故正交场的宽度L恰好等于2R时交变电场
均恒定不变,故正交场的宽度L恰好等于2R时交变电场![]() 的周期T最小,如图乙所示
的周期T最小,如图乙所示
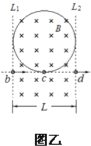
微粒从图中b运动到c所用的时间
![]()
故电场E2变化周期T的最小值
![]()

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目