��Ŀ����
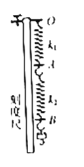
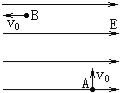
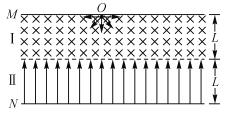
����Ŀ����ͼ��ʾ������I���ڴ�ֱ��ֽ���������ǿ�ų����Ÿ�Ӧǿ��ΪB��������������ֱ���ϵ���ǿ�糡���糡ǿ��ΪE��������ˮƽ�����㹻������ֱ����ĸ߶Ⱦ�ΪL���ڴų����ϱ߽��O�����һ������Դ��������Դ���ϵ����������������Ϊm�������Ϊq�Ĵ���������ӣ��������ӵķ������ʾ���ȡ�����M��λ�ڴų��ϱ߽磬N��λ�ڵ糡�±߽硣������ˮƽ��������ų������Ӵ�ֱ����N���ϵ�A�㣨ͼ��δ�������������������������Ӽ�����ã���
��1�����ӵķ�������v��
��2������N����������ڴų����˶������ʱ��t��
��3�����Ӵ���N�������x��
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��![]() .
.
��������
��1����ֱ����N��������ڴų��й���뾶
r=L
���������ṩ����������ţ�ٵڶ����ɵ�
![]()
��������ٶ�
![]()
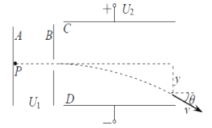
��2������N��������ڴų����˶������ʱ��t����ͼ��ʾ
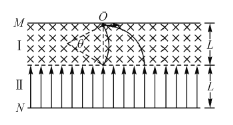
�ɼ��ι�ϵ��
��=60��
�����ڴų����˶�������
![]()
![]()
�˶�ʱ��
![]()
���
![]()
��3��������ˮƽ��������������������Ҳࣻ��������ֱ��������ų���������������.
��ͼ��ʾ��ֱ���������ڵ糡������ƽ���˶���

��ֱ����
![]()
ˮƽ����
x1=vt
N���ϳ�����������
x=2L+x1
���
![]()

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�