题目内容
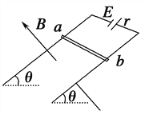
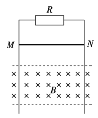
【题目】如图所示，有两个相互平行间距为L的金属导轨PQ和MN，磁感应强度大小为B的匀强磁场垂直导轨向上(图中没有画出)，导轨与水平成夹角为θ=30°，在P和M间接有电阻R，金属棒CD垂直搭接在金属导轨上，金属棒质量为m，电阻为r。已知金属棒与导轨间的动摩擦因数为μ=
，重力加速度为g，导轨足够长，求：
(1)若给金属棒一个沿导轨向上、大小为F=3mg的恒力，金属棒运动位移s时达到最大速度，求此过程金属棒产生的焦耳热Q是多少?
(2)若给金属棒一个沿导轨向下的速度，使金属棒获得的初动能为EK0，运动位移x0时动能减小为初动能的
，金属棒沿导轨向下运动的最大位移是多少?
【答案】(1)
；(2）
【解析】
（1）金属棒速度最大时，受力平衡，由受力情况列出平衡方程；结合功能关系求解此过程金属棒产生的焦耳热；（2）根据加速度的定义式，结合微元法求解速度和位移的关系，列式求解金属棒的最大位移.
（1） 金属棒的最大速度为vm时电动势E=BLvm；
此时回路中电流
受到的安培力为FA=BIL；
金属棒达最大速度时匀速运动：
;
对金属棒，在此过程中回路的焦耳热设为Q，由能量关系可知：
；
根据串联电路的特点可知：
联立解得：
（2）设金属棒初速度v1，运动位移x0时速度为v2，则有
由题意
和θ=300可知金属棒受到重力沿斜面向下的分力mgsinθ与其受到的滑动摩擦力μmgcosθ相平衡，金属棒在向下运动的过程中受到合外力就等于金属棒受到的沿导轨向上的安培力
，
金属棒的加速度大小为
即
金属棒沿导轨向下做减速运动，把金属棒的运动过程分成无数个小过程，每个过程均可视为匀速运动，设速度为v，则此过程的时间为t，根据加速度定义可知此过程的速度增量v=at，即
，
又每个小过程可视为匀速运动，可知此过程的运动位移为x=vt；由以上两式联立可知：
;
把整个过程都应用，并且把各个小过程相加可得：
,其中v0和vt分别为运动位移x的初速度和末速度；
对金属棒，从开始到运动位移x0的过程，有
；
对金属棒，从开始到速度减为零，设运动位移为xm，则
联立解得：xm=
x0
