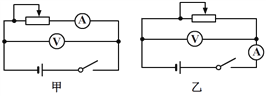
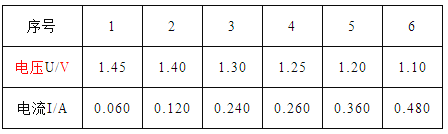
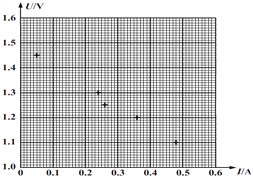
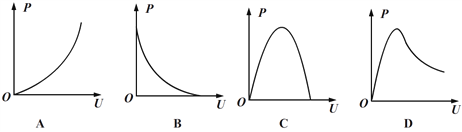
��Ŀ����
����Ŀ����ͼ��ʾ������ab�����ڹ⻬��ˮƽ�����ϣ�a��b�ϱ���ˮƽ����a��b�Ϸֱ����������d��c��a��b��������ϸ����������ʼϸ�߸պñ���ֱ����ʱϸ��ˮƽ����֪b��c֮���a��d֮�䶯Ħ��������Ϊ��������a��b��c��d��������Ϊm������dͨ������ϸ���ƹ��⻬������С����e������������סe��d�뻬�ּ��ϸ�߸պ���ֱ��ˮƽ��e������ľ���Ϊh��Ҫ��a��b��c��d��Ծ�ֹ���ͷ�����������ʹ������̵�ʱ�䵽����档��֪���Ħ������С���ڻ���Ħ��������
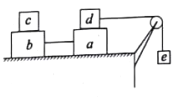
(1)c����������ʱ��?
(2)��ʱ����e������?
���𰸡�(1)![]() ��(2)
��(2)![]()
��������
��1������������˶��������ٶȣ�����˶���ʽ���c����������ʱ�䣻��2�����������뷨��ʽ�������e������.
��1��a��d֮��ľ�Ħ������a��b��c������������˶��Ķ����������ֵΪFm=��mg��
���˶��������ٶ�Ϊ![]() ��
��
��e������ľ���hһ�������ٶ�����˶���ʱ����̣������ʱ��Ϊtm,����h=![]() atm2�����
atm2����� ![]()
��2������abc��֪�����ٶ�![]() ��
��
������e��Meg-F=Mea��
������abcd������F=4ma
���![]()

��ϰ��ϵ�д�
 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
�����Ŀ