题目内容



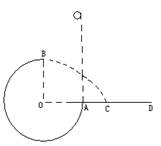
如图所示，竖直平面内的3/4圆弧形光滑轨道半径为R、A端与圆心O等高，AD为水平面，B端在O的正上方，一个小球自A点正上方由静止释放，自由下落至A点进入圆轨道并恰能到达B点，求：
(1)释放点距A点的竖直高度；
(2)落点C与A点的水平距离；

（1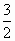） R    （2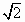）(－1)R

(1)由机械能守恒定律得
　　mgh＝mgR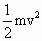＋　　①
　　因为恰能到B点则mg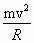＝　　②
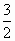　　∴h＝R
(2)设落点C与A水平距离为x，由平抛规律得：
　　R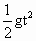＝　　③
　　R＋x＝vt　　④
　　∴x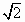＝(－1)R
练习册系列答案
相关题目
（10分）如图所示，一质量为m的滑块以大小为v0的速度经过水平直轨道上的a点滑行距离为s后开始沿竖直平面的半圆形轨道运动，滑块与水平直轨道间的动摩擦因数为μ，水平直轨道与半圆形轨道相切连接，半圆形轨道半径为R，滑块到达半圆形轨道最高点b时恰好不受压力．试求：
（1）滑块刚进入和刚离开半圆形轨道时的速度；
（2）滑块落回到水平直轨道时离a点的距离．
如图7-7-4所示，小球在倾角为30°的斜面上的A点水平抛出，抛出时的动能为6 J，则落到斜面上B点时的动能为(   )

图7-7-4
A．12 JB．14 JC．16 JD．18 J
如图7-7-6所示，一粗细均匀的U形管内装有同种液体且竖直放置，右管口用盖板A密封一部分气体，左管开口，两液面高度差为h，U形管中液柱总长为4h.现拿去盖板，液柱开始流动，不计水的粘滞阻力，当两侧管内液面恰好相齐时，右侧液面下降的速度大小为________.

图7-7-6
如图所示，完全相同的A、B两物块随足够长的水平传送带按图中所示方向匀速运动．A、B间夹有少量炸药，某时刻炸药爆炸，则（   ）
A．炸药爆炸后瞬间，A、B两物块速度方向一定相同
B．炸药爆炸后瞬间，A、B两物块速度方向一定相反
C．炸药爆炸过程中，A、B两物块组成的系统机械能守恒
D．炸药爆炸过程中，A、B两物块组成的系统机械能不守恒


如图，用长为L的细线悬挂一质量为m的小球，再把小球拉至A点，使悬线与水平方向成30°角．然后松手，使小球由静止开始运动，求小球运动到悬点的正下方B点时，悬线对小球的拉力多大?



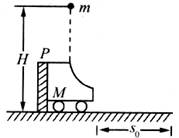
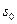质量为M的小车静止在光滑的水平面上，小车的上表面是一光滑的曲面，末端是水平的，如下图所示，小车被挡板P挡住，质量为优的物体从距地面高H处自由下落，然后沿光滑的曲面继续下滑，物体落地点与小车右端相距，若撤去挡板P，物体仍从原处自由落下，求物体落地时落地点距离小车右端多远？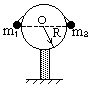


如图，半径为R的光滑圆柱体由支架固定在高处，用一条轻而细的绳将质量分别为的两小物体连结(图中虚线水平，且与一直径重合)，初始位置如图所示，已知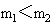，试讨论：当同时由静止释放后，质量为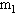的物体能通过圆柱体的最高点，且对圆柱体有压力的条件(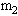到达最高点时尚未落地)．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网