题目内容
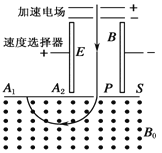
【题目】如图所示,在Ⅰ区里有与水平方向成60°角的匀强电场![]() ,宽度为d。在Ⅱ区里有垂直于纸面向外的匀强磁场和竖直方向的电场
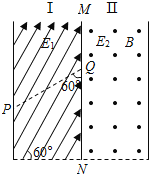
,宽度为d。在Ⅱ区里有垂直于纸面向外的匀强磁场和竖直方向的电场![]() ,宽度也为d。一带电量为q、质量为m 的微粒自图中P点由静止释放后沿虚线做直线运动进入Ⅱ区的磁场,已知PQ与中间边界MN的夹角是60°。若微粒进入Ⅱ区后做匀速圆周运动且还能回到MN边界上。重力加速度为g。Ⅰ区和Ⅱ区的场在竖直方向足够长,d、m、q已知,求:
,宽度也为d。一带电量为q、质量为m 的微粒自图中P点由静止释放后沿虚线做直线运动进入Ⅱ区的磁场,已知PQ与中间边界MN的夹角是60°。若微粒进入Ⅱ区后做匀速圆周运动且还能回到MN边界上。重力加速度为g。Ⅰ区和Ⅱ区的场在竖直方向足够长,d、m、q已知,求:
(1)微粒带何种电荷,电场强度![]() ;
;
(2)Ⅱ区磁感应强度B的取值范围;
(3)微粒第一次在磁场中运动的最长时间。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)带电微粒沿虚线做直线运动,微粒受重力和电场力
电场力F=qE1
由力的平行四边行定则和几何关系得F=![]() mg
mg
解得![]()
(2)由微粒在Ⅰ区的受力分析可知 F合=mg
微粒从![]() 到
到![]() 由动能定理得
由动能定理得 ![]()
而![]()
解得![]()
因微粒还能回到MN边界上,所以微粒在Ⅱ区最大圆与最右边界相切,由几何关系得圆的半径![]()
由牛顿第二定律 ![]()
解得![]()
(3)微粒在磁场中运动的周期![]()
联立得![]()
由此可知![]() 越小周期越长,所以当
越小周期越长,所以当![]() 时,粒子在磁场中运动周期最长;由几何关系得粒子从进入磁场到返回MN边界转过的圆心角
时,粒子在磁场中运动周期最长;由几何关系得粒子从进入磁场到返回MN边界转过的圆心角![]()
微粒第一次在磁场中运动的最长时间![]()
解得 ![]()

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目