题目内容
2. 长为L的导体棒原来不带电,将一带电量为q的点电荷放在棒左端R处,静电力常量为k,如图,当达到静电平衡后棒上感应的电荷在棒内中点处产生的场强的大小为$\frac{kq}{{(R+\frac{L}{2})}^{2}}$,方向水平向左.
长为L的导体棒原来不带电,将一带电量为q的点电荷放在棒左端R处,静电力常量为k,如图,当达到静电平衡后棒上感应的电荷在棒内中点处产生的场强的大小为$\frac{kq}{{(R+\frac{L}{2})}^{2}}$,方向水平向左.
分析 当棒达到静电平衡后,棒内各点的合场强为零,即感应电荷产生的电场强度与+q产生的电场强度大小相等、方向相反,根据静电平衡的特点和点电荷场强公式E=k$\frac{Q}{{r}^{2}}$结合求解.
解答 解:水平导体棒当达到静电平衡后,棒上感应电荷中点P处产生的场强大小与点电荷+q在该处产生的电场强度大小相等,方向相反.
则棒上感应电荷在棒内中点产生的场强大小为:$E=\frac{kq}{(R+\frac{L}{2})^{2}}$,
由于P处的合场强为零,所以感应电荷产生的场强方向与点电荷+q在该处产生的电场强度的方向相反,即水平向左.
故答案为:$\frac{kq}{{(R+\frac{L}{2})}^{2}}$,水平向左
点评 感应带电的本质是电荷的转移,当金属导体处于电场时会出现静电平衡现象,关键要理解并掌握静电平衡的特点.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
12. 如图所示,是某同学站在压力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿,横轴的单位为时间.由图可知( )
如图所示,是某同学站在压力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿,横轴的单位为时间.由图可知( )
 如图所示,是某同学站在压力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿,横轴的单位为时间.由图可知( )
如图所示,是某同学站在压力传感器上,做下蹲-起立的动作时记录的力随时间变化的图线,纵坐标为力(单位为牛顿,横轴的单位为时间.由图可知( )| A. | 该同学做了两次下蹲-起立的动作 | |
| B. | 该同学做了一次下蹲-起立的动作 | |
| C. | 下蹲过程中人处于失重状态 | |
| D. | 下蹲过程中先处于超重状态后处于失重状态 |
13.发射卫星时将卫星发射至近地圆轨道经变轨后进入预定轨道.现一人造地球卫星绕地球做匀速圆周运动,假如该卫星变轨后仍做匀速圆周运动,动能减小为原来的$\frac{1}{4}$,不考虑卫星质量的变化,则变轨前后卫星的( )
| A. | 周期之比为1:8 | B. | 角速度之比为2:1 | ||
| C. | 向心加速度大小之比为4:1 | D. | 轨道半径之比为1:2 |
10. 如图示,在正点电荷Q形成的电场中,AD,BC是以Q为圆心的两段圆弧,正点电荷q沿A→B→C→D→A移动,则该电荷q( )
如图示,在正点电荷Q形成的电场中,AD,BC是以Q为圆心的两段圆弧,正点电荷q沿A→B→C→D→A移动,则该电荷q( )
 如图示,在正点电荷Q形成的电场中,AD,BC是以Q为圆心的两段圆弧,正点电荷q沿A→B→C→D→A移动,则该电荷q( )
如图示,在正点电荷Q形成的电场中,AD,BC是以Q为圆心的两段圆弧,正点电荷q沿A→B→C→D→A移动,则该电荷q( )| A. | 沿BC运动时不受电场力 | |
| B. | 沿DA运动时电场力不做功 | |
| C. | 在B点时的电势能比在D点时的小 | |
| D. | 在A点时受到的电场力比在C点时的小 |
17.在绝缘水平面上放着带电小球甲和乙,若它们的带电荷量的关系是q甲=4q乙,则它们所受库仑力的大小之比是( )
| A. | F甲:F乙=1:4 | B. | F甲:F乙=4:1 | C. | F甲:F乙=1:1 | D. | F甲:F乙=16:1 |
7.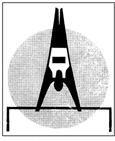 运动员在单杠上处于如下图所示的平衡状态,两只手臂的夹角为60°,已知该运动员体重为600N,则手臂的支持力约为( )
运动员在单杠上处于如下图所示的平衡状态,两只手臂的夹角为60°,已知该运动员体重为600N,则手臂的支持力约为( )
 运动员在单杠上处于如下图所示的平衡状态,两只手臂的夹角为60°,已知该运动员体重为600N,则手臂的支持力约为( )
运动员在单杠上处于如下图所示的平衡状态,两只手臂的夹角为60°,已知该运动员体重为600N,则手臂的支持力约为( )| A. | 300N | B. | 200$\sqrt{3}$N | C. | 400N | D. | 600N |
11.有一辆汽车刹车后做匀减速直线运动的v-t图象如图所示,则下列说法正确的是( )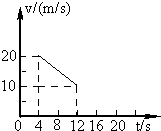

| A. | 汽车开始刹车时的速度为25m/s | B. | 汽车刹车后的速度每1s减小5m/s | ||
| C. | 4s~12s内汽车的位移为120m | D. | 刹车后经25s速度减为零 |
 如图是高频焊接原理示意图,线圈中通以高频交流电时,待焊接的金属工件中就产生感应电流,由于焊缝处的接触电阻很大,放出的焦耳热很多,致使温度升得很高,将金属熔化,焊接在一起.我国生产的自行车车架就是用这种办法焊接的.试定性地说明:为什么交变电流的频率越高,焊缝处放出的热量越多.
如图是高频焊接原理示意图,线圈中通以高频交流电时,待焊接的金属工件中就产生感应电流,由于焊缝处的接触电阻很大,放出的焦耳热很多,致使温度升得很高,将金属熔化,焊接在一起.我国生产的自行车车架就是用这种办法焊接的.试定性地说明:为什么交变电流的频率越高,焊缝处放出的热量越多.