Question

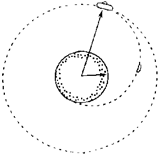我国的“嫦娥奔月”月球探测工程已经启动，分“绕、落、回”三个发展阶段：在2007年发射一颗绕月球飞行的卫星在2012年前后发射一颗月球软着陆器；在2017年前后发射一颗返回式月球软着陆器，进行首次月球样品自动取样并安全返回地球，设想着陆器完成了对月球表面的考察任务后，由月球表面回到围绕月球做圆周运动的轨道舱，其过程如图所示．设轨道舱的质量为m，月球表面的重力加速度为g，月球的半径为R，轨道舱到月球中心的距离为r，引力常量为G，则试求：
（1）月球的质量；
（2）轨道舱的速度和周期．

Answer 1

分析：（1）着陆器在月球表面上的重力等于万有引力，列式可得到月球的质量．
（2）轨道舱绕月球做圆周运动，由月球的万有引力提供向心力，根据牛顿第二定律，列式求解速度、周期．

解答：解：（1）设月球的质量为M，着陆器的质量为m₀
着陆器在月球表面上的重力等于万有引力：m₀g=G

Mm0

R2

解得，M=

gR2

G

．
（2）轨道舱绕月球做圆周运动，由万有引力提供向心力，则得：
 G

Mm

r2

=m

v2

r

解得，v=

GM r

=

gR2 r

周期为 T=

2πr

v

=2πr

r GM

=2πr

r gR2

答：（1）月球的质量是

gR2

G

；（2）轨道舱的速度是

gR2 r

，周期为2πr

r gR2

．

点评：本题要建立清晰的运动模型，利用万有引力等于重力，万有引力等于向心力，进行求解．