题目内容
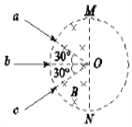
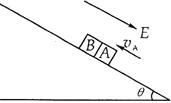
【题目】在倾角为θ的足够长的绝缘斜面上，带负电的物块A和不带电的绝缘物块B正分别沿斜面向上滑行。斜面处于范围足够大的匀强电场中，场强方向平行斜面向下。当A刚要追上B时，物块A的速度vA＝1.8m/s，方向沿斜面向上，物块B的速度恰为零，如图所示。A、B碰撞过程相互作用时间极短，且A的电荷没有转移。碰后瞬间A的速度v1＝0.6m/s，方向仍沿斜面向上。碰后经0.60s，物块A的速率变为v2＝1.8m/s，在这0.60s时间内两物块没有再次相碰。己知物块A和斜面间的动摩擦因数μ＝0.15，物块B与斜面间的摩擦可忽略不计，物块A、B均可视为质点，它们质量分别为mA＝0.5Kg，mB＝0.25kg，匀强电场的场强E＝5×106N/C，sinθ＝0.6，重力加速度g＝10m/s2。
（1）第一次碰后的0.6s内物块B沿斜面向上最多能滑多远?
（2）分析第一次碰撞后至0.60s这段时间内A的运动方向，并求出A的电荷量？
（3）分析第一次碰撞后至0.60s这段时间内，物块A的电势能的变化情况？
【答案】（1）0.48m（2）-1.2×10-7C（3）电势能减少了0.252J
【解析】（1）A、B碰撞时间极短，沿斜面方向动量守恒。设碰后瞬间B的速度为vB，由动量守恒定律，有
解得 
碰撞后物块B的加速度为 
，方向沿斜面向下
B沿斜面上滑到最高点用的时为 
所以，第一次碰后的0.6s内，B沿斜面上滑的最远距离为 
1分
（2）碰后的0.6s内，A的运动有两种可能：①一直加速向上；②减速向上再加速向下
设A的加速度为aA
第①种情况：以沿斜面向上的方向为正，A的加速度 
设经t’时间第二次相遇，两物位移相等，即 
解得 t’＝0.45s＜0.6s，不合题意，所以A的运动只能是第②种情况。
以沿斜面向下的方向为正，设物块A碰撞后向上减速运动的加速度大小为a1，向下加速运动时的加速度大小为a2。A受到的电场力为F。由题意得 
分别对上滑和下滑过程运用牛顿第二定律列方程
上滑过程： 
下滑过程： 
联立上述方程得 F＝-0.6N或-3.4N（舍）、
电荷量为 
（3）由
可得 物块A上滑的位移大小为 
物块下滑的位移大小为 
故在0.60s时间内物块A的总位移为 
，方向向下
电场力做功为 
物块A的电势能减少了 
