题目内容
19. 用一根细线一端系一小球(可视为质点),另一端固定在一光滑圆锥体顶部,如图所示.设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图象是( )
用一根细线一端系一小球(可视为质点),另一端固定在一光滑圆锥体顶部,如图所示.设小球在水平面内作匀速圆周运动的角速度为ω,线的张力为T,则T随ω2变化的图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 分析小球的受力,判断小球随圆锥作圆周运动时的向心力的大小,进而分析T随ω2变化的关系,但是要注意的是,当角速度超过某一个值的时候,小球会飘起来,离开圆锥,从而它的受力也会发生变化,T与ω2的关系也就变了.
解答 解:设绳长为L,锥面与竖直方向夹角为θ,当ω=0时,小球静止,受重力mg、支持力N和绳的拉力T而平衡,T=mgcosθ≠0,所以A项、B项都不正确;
ω增大时,T增大,N减小,当N=0时,角速度为ω0.
当ω<ω0时,由牛顿第二定律得,
Tsinθ-Ncosθ=mω2Lsinθ,
Tcosθ+Nsinθ=mg,
解得T=mω2Lsin2θ+mgcosθ;
当ω>ω0时,小球离开锥子,绳与竖直方向夹角变大,设为β,由牛顿第二定律得
Tsinβ=mω2Lsinβ,
所以T=mLω2,
可知T-ω2图线的斜率变大,所以C项正确,D错误.
故选:C.
点评 本题很好的考查了学生对物体运动过程的分析,在转的慢和快的时候,物体的受力会变化,物理量之间的关系也就会变化.

练习册系列答案
相关题目
9. 如图,真空中存在竖直向上的匀强电场和水平方向的匀强磁场,质量为m、电荷量为q的物体以速率v在场内做半径为R的匀速圆周运动,设t=0时物体在轨道最低点且重力势能和电势能均为零,则下列判断正确的是( )
如图,真空中存在竖直向上的匀强电场和水平方向的匀强磁场,质量为m、电荷量为q的物体以速率v在场内做半径为R的匀速圆周运动,设t=0时物体在轨道最低点且重力势能和电势能均为零,则下列判断正确的是( )
 如图,真空中存在竖直向上的匀强电场和水平方向的匀强磁场,质量为m、电荷量为q的物体以速率v在场内做半径为R的匀速圆周运动,设t=0时物体在轨道最低点且重力势能和电势能均为零,则下列判断正确的是( )
如图,真空中存在竖直向上的匀强电场和水平方向的匀强磁场,质量为m、电荷量为q的物体以速率v在场内做半径为R的匀速圆周运动,设t=0时物体在轨道最低点且重力势能和电势能均为零,则下列判断正确的是( )| A. | 物体一定带正电且逆时针运动 | |
| B. | 物体运动过程中,机械能守恒且恒为$\frac{1}{2}$mv2 | |
| C. | 物体运动过程中,重力势能随时间变化关系为mgR(1-cos$\frac{v}{R}$t) | |
| D. | 物体运动过程中,电势能随时间变化关系为mgR(cos$\frac{v}{R}$t-1) |
7. 如图所示的圆形线圈共n匝,电阻为R,过线圈中心O垂直于线圈平面的直线上有A、B两点,A、B两点的距离为L,A、B关于O点对称.一条形磁铁开始放在A点,中心与O点重合,轴线与A、B所在直线重合,此时线圈中的磁通量为φ1,将条形磁铁以速度v匀速向右移动,轴线始终与直线重合,磁铁中心到O点时线圈中的磁通量为φ2,下列说法正确的是( )
如图所示的圆形线圈共n匝,电阻为R,过线圈中心O垂直于线圈平面的直线上有A、B两点,A、B两点的距离为L,A、B关于O点对称.一条形磁铁开始放在A点,中心与O点重合,轴线与A、B所在直线重合,此时线圈中的磁通量为φ1,将条形磁铁以速度v匀速向右移动,轴线始终与直线重合,磁铁中心到O点时线圈中的磁通量为φ2,下列说法正确的是( )
 如图所示的圆形线圈共n匝,电阻为R,过线圈中心O垂直于线圈平面的直线上有A、B两点,A、B两点的距离为L,A、B关于O点对称.一条形磁铁开始放在A点,中心与O点重合,轴线与A、B所在直线重合,此时线圈中的磁通量为φ1,将条形磁铁以速度v匀速向右移动,轴线始终与直线重合,磁铁中心到O点时线圈中的磁通量为φ2,下列说法正确的是( )
如图所示的圆形线圈共n匝,电阻为R,过线圈中心O垂直于线圈平面的直线上有A、B两点,A、B两点的距离为L,A、B关于O点对称.一条形磁铁开始放在A点,中心与O点重合,轴线与A、B所在直线重合,此时线圈中的磁通量为φ1,将条形磁铁以速度v匀速向右移动,轴线始终与直线重合,磁铁中心到O点时线圈中的磁通量为φ2,下列说法正确的是( )| A. | 磁铁在A点时,通过一匝线圈的磁通量为$\frac{{φ}_{1}}{n}$ | |
| B. | 磁铁从A到O的过程中,线圈中产生的平均感应电动势为$\frac{2πv({φ}_{1}-{φ}_{2})}{L}$ | |
| C. | 磁铁从A到B的过程中,线圈中磁通量的变化量为2φ1 | |
| D. | 磁铁从A到B的过程中,通过线圈某一截面的电量不为零 |
14. 如图所示,正方形abcd区域内分布着垂直纸面向里的匀强磁场,O点是cd边的中点.一个带正电的粒子仅在磁场力的作用下,从O点沿纸面以垂直于cd边的速度射入磁场,经过时间t0刚好从c点射出磁场.现让该粒子从O点沿纸面以与Od成30°角的方向,分别以大小不同的速率射入磁场,则关于该粒子在磁场中运动的时间t和离开正方形区域位置,分析正确的是( )
如图所示,正方形abcd区域内分布着垂直纸面向里的匀强磁场,O点是cd边的中点.一个带正电的粒子仅在磁场力的作用下,从O点沿纸面以垂直于cd边的速度射入磁场,经过时间t0刚好从c点射出磁场.现让该粒子从O点沿纸面以与Od成30°角的方向,分别以大小不同的速率射入磁场,则关于该粒子在磁场中运动的时间t和离开正方形区域位置,分析正确的是( )
 如图所示,正方形abcd区域内分布着垂直纸面向里的匀强磁场,O点是cd边的中点.一个带正电的粒子仅在磁场力的作用下,从O点沿纸面以垂直于cd边的速度射入磁场,经过时间t0刚好从c点射出磁场.现让该粒子从O点沿纸面以与Od成30°角的方向,分别以大小不同的速率射入磁场,则关于该粒子在磁场中运动的时间t和离开正方形区域位置,分析正确的是( )
如图所示,正方形abcd区域内分布着垂直纸面向里的匀强磁场,O点是cd边的中点.一个带正电的粒子仅在磁场力的作用下,从O点沿纸面以垂直于cd边的速度射入磁场,经过时间t0刚好从c点射出磁场.现让该粒子从O点沿纸面以与Od成30°角的方向,分别以大小不同的速率射入磁场,则关于该粒子在磁场中运动的时间t和离开正方形区域位置,分析正确的是( )| A. | 若t=$\frac{5}{3}$t0,则它一定从dc边射出磁场 | |
| B. | 若t=$\frac{5}{4}$t0,则它一定从cb边射出磁场 | |
| C. | 若t=t0,则它一定从ba边射出磁场 | |
| D. | 若t=$\frac{2}{3}$t0,则它一定从da边射出磁场 |
11.三束单色光a、b、c沿图示方向射向圆形玻璃砖,经两次折射后变成复色光d,以下说法正确的是( )
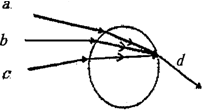

| A. | 在真空中,a光传播速度比b、c大 | |
| B. | b光的频率比c光小 | |
| C. | a光的光子能量最小 | |
| D. | 在玻璃砖中,a光传播速度比b、c小 | |
| E. | 若以a、b、c三种单色光分别用相同的装置做“用双缝干涉测定单色光的波长”的实验,则a光观察到的条纹间距最大 |
9. 如图,在光滑绝缘的倾角为30°的斜面内有平行斜面的水平匀强磁场,长为l的轻绳一端固定在O点另一端系一带电小球,使小球恰能在斜面内做圆周运动.已知其所受电场力等于重力的一半,小球质量为m,重力加速度为g.则( )
如图,在光滑绝缘的倾角为30°的斜面内有平行斜面的水平匀强磁场,长为l的轻绳一端固定在O点另一端系一带电小球,使小球恰能在斜面内做圆周运动.已知其所受电场力等于重力的一半,小球质量为m,重力加速度为g.则( )
 如图,在光滑绝缘的倾角为30°的斜面内有平行斜面的水平匀强磁场,长为l的轻绳一端固定在O点另一端系一带电小球,使小球恰能在斜面内做圆周运动.已知其所受电场力等于重力的一半,小球质量为m,重力加速度为g.则( )
如图,在光滑绝缘的倾角为30°的斜面内有平行斜面的水平匀强磁场,长为l的轻绳一端固定在O点另一端系一带电小球,使小球恰能在斜面内做圆周运动.已知其所受电场力等于重力的一半,小球质量为m,重力加速度为g.则( )| A. | 小球的最小速率为$\sqrt{gl}$ | B. | 小球的最小速率为$\sqrt{\frac{gl}{2}}$ | ||
| C. | 绳中最大拉力为5.5mg | D. | 绳中最大拉力为3$\sqrt{2}$mg |
 如图所示是A、B两个相同的圆柱形气缸,放置在同-水平面内,气缸壁及活塞导热良好,气缸内均封闭有一定质量的气体.当二者均在温度为27℃的环境中,两活塞静止不动时的高度差为h.则当二者均处于温度为127℃的环境中,两活塞静止不动时的高度差为多少?(设活塞与气缸壁之间摩擦不计,活塞质量不计,27℃和127℃两个环境下的压强相同)
如图所示是A、B两个相同的圆柱形气缸,放置在同-水平面内,气缸壁及活塞导热良好,气缸内均封闭有一定质量的气体.当二者均在温度为27℃的环境中,两活塞静止不动时的高度差为h.则当二者均处于温度为127℃的环境中,两活塞静止不动时的高度差为多少?(设活塞与气缸壁之间摩擦不计,活塞质量不计,27℃和127℃两个环境下的压强相同) 如图所示,水平放置的轻弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为Ep=28J.撤去推力后,P沿桌面滑到一个上表面与桌面等高且静止在光滑水平地面上的长木板Q上,已知P、Q的质量均为m=2kg,A、B间的距离L1=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求
如图所示,水平放置的轻弹簧左端固定,小物块P(可视为质点)置于水平桌面上的A点,并与弹簧右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢地推至B点,此时弹簧的弹性势能为Ep=28J.撤去推力后,P沿桌面滑到一个上表面与桌面等高且静止在光滑水平地面上的长木板Q上,已知P、Q的质量均为m=2kg,A、B间的距离L1=4m,A距桌子边缘C的距离L2=2m,P与桌面及P与Q间的动摩擦因数都为μ=0.1,g取10m/s2,求 如图所示,质量为m的劈A和质量为m的物体B静止在光滑水平面上,物体B左端固定轻质弹簧,一质量为m的小球C从距离水平面高度h处从劈光滑的弧面滑下,求运动过程中弹簧的最大弹性势能?
如图所示,质量为m的劈A和质量为m的物体B静止在光滑水平面上,物体B左端固定轻质弹簧,一质量为m的小球C从距离水平面高度h处从劈光滑的弧面滑下,求运动过程中弹簧的最大弹性势能?