Question

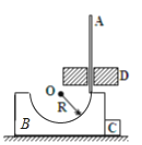
【题目】如图所示，在光滑水平地面上有一固定的挡板，挡板左端定一个轻弹簧。小车AB的质量M=3kg，长L=4m(其中O为小车的中点，AO部分粗糙，BO部分光滑)，一质量为m=1kg的小物块(可视为质点)，放在小车的最左端，车和小物块一起以v0=4m/s的速度在水平面上向右匀速运动，车撞到挡板后瞬间速度变为零，但未与挡板粘连。已知车OB部分的长度大于弹簧的自然长度，小物块与弹簧作用过程中弹簧始终处于弹性限度内，小物块与小车AO部分之间的动摩擦因数为μ=0.3，重力加速度取10m/s2。求

(1)小物块和弹簧相互作用的过程中，弹簧具有的最大弹性势能；

(2)小物块和弹簧相互作用的过程中，弹簧对小物块的冲量；

(3)小物块最终停在小车上的位置距A端多远。

Answer 1

【答案】（1）2J；（2）4kgm/s，水平向右；（3）1.5m；

【解析】（1）对小物块，有ma=-μmg
根据运动学公式v2v02＝2a
由能量关系mv2＝Ep，
解得EP=2J．
（2）设小物块离开弹簧时的速度为v1，有mv12＝Ep．
对小物块，根据动量定理I=-mv1-mv
由⑤⑥式并代入数据得I=-4kgm/s．
弹簧对小物块的冲量大小为4kgm/s，方向水平向左．
（3）小物块滑过O点和小车相互作用，由动量守恒mv1=（m+M）v2．
由能量关系μmgx＝mv12 (m+M)v22
小物块最终停在小车上距A的距离xA＝x
解得xA=1.5m．