题目内容
 (2012?东城区模拟)如图所示在足够长的光滑水平面上有一静止的质量为M的斜面,斜面表面光滑、高度为h、倾角为θ.一质量为m(m<M)的小物块以一定的初速度沿水平面向右运动,不计冲上斜面过程中的机械能损失.如果斜面固定,则小物块恰能冲到斜面的顶端.如果斜面不固定,则小物块冲上斜面后能达到的最大高度为( )
(2012?东城区模拟)如图所示在足够长的光滑水平面上有一静止的质量为M的斜面,斜面表面光滑、高度为h、倾角为θ.一质量为m(m<M)的小物块以一定的初速度沿水平面向右运动,不计冲上斜面过程中的机械能损失.如果斜面固定,则小物块恰能冲到斜面的顶端.如果斜面不固定,则小物块冲上斜面后能达到的最大高度为( )分析:斜面固定时,由动能定理求出初速度,斜面不固定时,由水平方向动量守恒列式,再根据机械能守恒列式,联立方程即可求解.
解答:解:斜面固定时,由动能定理得:
-mgh=0-
mv02,
所以v0=
;
斜面不固定时,由水平方向动量守恒得:
mv0=(M+m)v,
由机械能守恒得:
mv02=
(M+m)v 2+mgh′
解得:h′=
h.
故选D
-mgh=0-
| 1 |
| 2 |
所以v0=
| 2gh |
斜面不固定时,由水平方向动量守恒得:
mv0=(M+m)v,
由机械能守恒得:
| 1 |
| 2 |
| 1 |
| 2 |
解得:h′=
| M |
| M+m |
故选D
点评:本题主要考查了动能定理、动量守恒定律及根据机械能守恒的直接应用,难度适中.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
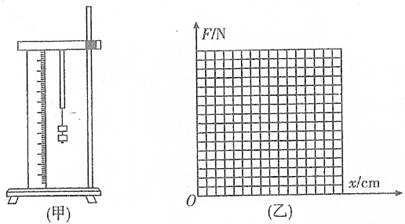 (2012?东城区模拟)橡皮筋也像弹簧一样,在弹性限度内伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实际都表明k=
(2012?东城区模拟)橡皮筋也像弹簧一样,在弹性限度内伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实际都表明k=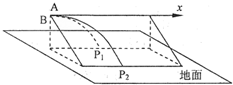 (2012?东城区一模)如图所示,A、B两质点从同一位置以相同的水平初速v0抛出,A在竖直面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2,不计阻力,比较P1、P2在水平x轴方向上距抛出点的远近关系及落地时速度的大小关系,正确的是( )
(2012?东城区一模)如图所示,A、B两质点从同一位置以相同的水平初速v0抛出,A在竖直面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2,不计阻力,比较P1、P2在水平x轴方向上距抛出点的远近关系及落地时速度的大小关系,正确的是( )