题目内容
2.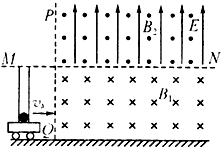 如图所示,水平地面上有一辆小车,车上固定一个竖直光滑绝缘管,管的底部有一质量m1=0.2g、电荷量q=8×10-5C的带正电小球,小球的直径比管的内径略小.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1=15T的匀强磁场,MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场,现让小车始终保持vx=2m/s的速度匀速向右运动,以带电小球刚经过磁场的边界PQ为计时的起点,测得小球在管内运动的这段时间为t=1s,g取10/s2,不计空气阻力.
如图所示,水平地面上有一辆小车,车上固定一个竖直光滑绝缘管,管的底部有一质量m1=0.2g、电荷量q=8×10-5C的带正电小球,小球的直径比管的内径略小.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1=15T的匀强磁场,MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场,现让小车始终保持vx=2m/s的速度匀速向右运动,以带电小球刚经过磁场的边界PQ为计时的起点,测得小球在管内运动的这段时间为t=1s,g取10/s2,不计空气阻力.(1)求小球进入磁场B1时的加速度a的大小.
(2)求小球离开管口时的速度v的大小.
(3)若小球离开管口后,在运动中的最高点,与静止在绝缘支架的微小光滑水平台上的、质量为m2=0.2g、不带电的小球(图中未画出)碰撞后成为一个整体,且碰撞导致该整体不带电.求该整体穿过MN平面的位置到小球刚离开管口时的位置之间的距离s的大小.
分析 (1)由洛伦兹力与重力共同提供合力,根据牛顿第二定律,即可求解;
(2)根据速度的分解,结合矢量法则,即可求解;
(3)因电场力与重力相平衡,则洛伦兹力提供向心力,结合牛顿第二定律、运动学公式,与几何关系,及动量守恒定律,即可求解.
解答 解:(1)小球在管中参与两个方向的运动,即水平方向,
以vx向右匀速运动,竖直方向,因水平速度而受到竖直向上的洛伦兹力,向上匀加速运动.
小球进入磁场B1时的加速度为a,由牛顿第二定律得:B1qvx-m1g=m1a,解得:a=2m/s2;
(2)小球在t=1s时,竖直分速度,vy=at=2m/s;而水平分速度vx=2m/s;
则小球离开管口的速度v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=2$\sqrt{2}$m/s;
(3)小球离开管子后,进入MN上方的复合场中,因Eq1=2×10-3N=m1g;
所以小球在洛伦兹力的作用下,做匀速圆周运动,设v与MN成θ角,
则tanθ=$\frac{{v}_{y}}{{v}_{x}}$=1,解得:θ=45°;
其运动的轨迹如图所示: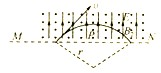
由牛顿第二定律得:
B2qv=m1$\frac{{v}^{2}}{r}$,解得:r=$\sqrt{2}$m,
当小球运动到最高点时,速度水平,与小球2碰撞,
水平方向动量守恒,且合成的整体不带电,此后做平抛运动,设共同速度为v1;
以向右为正方向,由动量守恒定律得:m1v=(m1+m2)v1,解得:v1=$\sqrt{2}$m/s,
设最高点距MN的距离为h,则有:h=r-rsin45°=($\sqrt{2}$-1)m;
设平抛运动的时间为t1,则有:h=$\frac{1}{2}$gt12,解得:t1=$\sqrt{\frac{\sqrt{2}-1}{5}}$,
所求距离s=rcos45°+v1t1;
解得:s=(1+$\sqrt{\frac{2(\sqrt{2}-1)}{5}}$)m≈1.4m.
答:(1)小球进入磁场B1时的加速度a的大小2m/s2.
(2)小球离开管口时的速度v的大小2$\sqrt{2}$m/s.
(3)该整体穿过MN平面的位置到小球刚离开管口时的位置之间的距离s的大小1.4m.
点评 考查洛伦兹力作用下做匀速圆周运动,理解牛顿第二定律的应用,掌握矢量的分解法则,注意几何关系的正确建立,掌握动量守恒定律,注意其方向性.

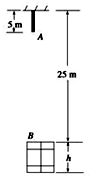 如图所示,有一根长L=5m的铁链悬挂在某楼顶上,楼中有一窗口,窗口上沿离铁链的悬点H=25m.当铁链从静止开始下落后始终保持竖直,不计空气阻力,g=10m/s2.则( )
如图所示,有一根长L=5m的铁链悬挂在某楼顶上,楼中有一窗口,窗口上沿离铁链的悬点H=25m.当铁链从静止开始下落后始终保持竖直,不计空气阻力,g=10m/s2.则( )| A. | 铁链的下端A下落到窗口的上沿B时,铁链的速度大小为20m/s | |
| B. | 接着铁链经过整个窗口用了t=0.3s的时间,窗口的高度h为0.45m | |
| C. | 若升高悬点的高度,铁链经过整个窗口所用时间变长 | |
| D. | 若升高悬点的高度,铁链经过整个窗口所用时间变短 |

| A. | 若增大R1,油滴加速上升 | B. | 若增大R2,油滴加速上升 | ||
| C. | 若增大R3,油滴加速上升 | D. | 若增大R4,油滴加速上升 |
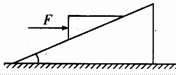 如图所示,一重物静止在粗糙斜面体上,斜面体固定在水平面上,现用一水平力F作用在该重物上,当水平力F从零逐渐增大的过程中( )
如图所示,一重物静止在粗糙斜面体上,斜面体固定在水平面上,现用一水平力F作用在该重物上,当水平力F从零逐渐增大的过程中( )| A. | 重物所受合力逐渐增大 | |
| B. | 斜面对重物的摩擦力逐渐增大 | |
| C. | 斜面对重物的弹力逐渐增大 | |
| D. | 当F增大到足够大时,重物一定沿斜面向上滑动 |

| A. | $\frac{{3p}_{0}L}{2S}$ | B. | $\frac{{p}_{0}L}{2S}$ | C. | $\frac{{p}_{0}L}{S}$ | D. | $\frac{{2p}_{0}L}{S}$ |
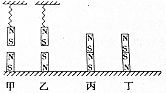
| A. | 对地面压力最大的是丙 | B. | 对地面压力最大的是甲 | ||
| C. | 对地面压力最大的是甲、丙、丁 | D. | 对地面压力最大的是丙、丁 |
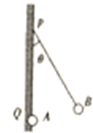 如图所示,竖直绝缘墙壁上的Q处有一固定的质点A,在Q正上方的P点用绝缘丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,使悬线与竖直方向成θ角,现通过某种方法使A、B的带电荷量均变为原来的两倍,则悬线对悬点P的拉力大小将( )
如图所示,竖直绝缘墙壁上的Q处有一固定的质点A,在Q正上方的P点用绝缘丝线悬挂另一质点B,A、B两质点因为带电而相互排斥,使悬线与竖直方向成θ角,现通过某种方法使A、B的带电荷量均变为原来的两倍,则悬线对悬点P的拉力大小将( )| A. | 变为原来的$\frac{1}{2}$ | B. | 保持不变 | C. | 变为原来的2倍 | D. | 变为原来的4倍 |
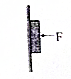 如图所示,重为G=10N的木块,被大小为F=40N的水平力压紧在竖直墙面上.木块静止,木块与墙面的动摩擦因素为μ=0.5.问:
如图所示,重为G=10N的木块,被大小为F=40N的水平力压紧在竖直墙面上.木块静止,木块与墙面的动摩擦因素为μ=0.5.问: 用单摆测重力加速度的实验中:
用单摆测重力加速度的实验中: