题目内容
14.计算匀变速直线运动的位移时,可作出运动的v-t图象,把运动时间分成很多很小的时间间隔,在每一很小的时间间隔内,质点的运动可看做匀速运动,位移大小为v-t图象中小矩形的面积大小,然后对所有小时间间隔的矩形面积大小求和,得到的时间内的位移大小等于图线与坐标轴所围面积大小.现有一根粗细均匀的导体棒AB,长度为L,横截面积为s,其电阻率从A到B逐渐变化,规律为ρ=ρ0(1+$\frac{x}{L}$).x为棒上各点到A端的距离.由以上方法可求该导体棒的总电阻为( )
| A. | $\frac{{3p}_{0}L}{2S}$ | B. | $\frac{{p}_{0}L}{2S}$ | C. | $\frac{{p}_{0}L}{S}$ | D. | $\frac{{2p}_{0}L}{S}$ |
分析 ρ-L图线与长度轴围成的面积表示导体的电阻与横截面积的乘积,根据图线面积求出电阻.
解答 解:根据题意,画出ρ-L图线的图象如图,可知,ρ-L图线与长度轴围成的面积表示导体的电阻与横截面积的乘积.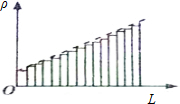
所以:$R•S=\frac{{ρ}_{0}[1+(1+\frac{L}{L})]}{2}•L=\frac{3{ρ}_{0}L}{2}$
所以:R=$\frac{{3p}_{0}L}{2S}$
故选:A
点评 该题属于对物理学方法的考查,解决本题的关键能结合速度时间图线的物理意义,将该方法迁移到ρ-L图线中,知道图线与L轴围成的面积表示的含义.属于中档题目.

练习册系列答案
相关题目
1.从某高处自由下落到地面的物体,在中间一秒内通过的路程为30米,则该物体下落时的高度为( )
| A. | 60米 | B. | 100米 | C. | 140米 | D. | 180米 |
2.在平直公路上,自行车与同方向行驶的一辆汽车在t=0时同时经过某一个路标,它们的位移s(m)随时间t(s)变化的规律为:汽车为s=10t-0.25t2,自行车为s=6t,则下列说法正确的是( )
| A. | 汽车作初速度为10m/s,加速度为0.5m/s2的匀减速直线运动 | |
| B. | 自行车作匀速直线运动,3s后的位移为24m | |
| C. | 汽车30s后的位移为75m | |
| D. | 两车相遇时距离路标96m |
6.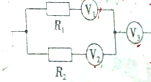 部分电路如图所示,三个电压表都相同,R1和R2为两个定值电阻,当这部分电路接通后,电压表2和3的示数分别为4V和10V,由此可判断出( )
部分电路如图所示,三个电压表都相同,R1和R2为两个定值电阻,当这部分电路接通后,电压表2和3的示数分别为4V和10V,由此可判断出( )
 部分电路如图所示,三个电压表都相同,R1和R2为两个定值电阻,当这部分电路接通后,电压表2和3的示数分别为4V和10V,由此可判断出( )
部分电路如图所示,三个电压表都相同,R1和R2为两个定值电阻,当这部分电路接通后,电压表2和3的示数分别为4V和10V,由此可判断出( )| A. | R1:R2=2:3 | B. | R1:R2:=3:2 | ||
| C. | 电压表V1的示数为6V | D. | 电压表V1的示数为4V |
3.在平直公路上行驶的a车和b车,其位移-时间图象分别为图中直线a和曲线b,由图可知( )
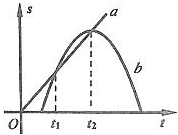

| A. | b车运动方向始终不变 | |
| B. | 在t1时刻a车与b车速度相同 | |
| C. | t1到t2时间内a车的平均速度小于b车 | |
| D. | t1到t2时间内有一时刻两车的速度相同 |
4.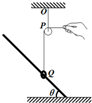 如图所示,将一直杆固定在地面上,与地面间夹角为θ.一光滑轻环套在杆上,一个大小和质量都不计的滑轮用轻绳OP悬挂在天花板上,用另一轻绳跨过滑轮系在轻环上,用手拉住轻绳另一端并使OP恰好在竖直方向,现水平向右缓慢拉绳至轻环重新静止,此时QP段轻绳与天花板之间所夹的锐角为( )
如图所示,将一直杆固定在地面上,与地面间夹角为θ.一光滑轻环套在杆上,一个大小和质量都不计的滑轮用轻绳OP悬挂在天花板上,用另一轻绳跨过滑轮系在轻环上,用手拉住轻绳另一端并使OP恰好在竖直方向,现水平向右缓慢拉绳至轻环重新静止,此时QP段轻绳与天花板之间所夹的锐角为( )
 如图所示,将一直杆固定在地面上,与地面间夹角为θ.一光滑轻环套在杆上,一个大小和质量都不计的滑轮用轻绳OP悬挂在天花板上,用另一轻绳跨过滑轮系在轻环上,用手拉住轻绳另一端并使OP恰好在竖直方向,现水平向右缓慢拉绳至轻环重新静止,此时QP段轻绳与天花板之间所夹的锐角为( )
如图所示,将一直杆固定在地面上,与地面间夹角为θ.一光滑轻环套在杆上,一个大小和质量都不计的滑轮用轻绳OP悬挂在天花板上,用另一轻绳跨过滑轮系在轻环上,用手拉住轻绳另一端并使OP恰好在竖直方向,现水平向右缓慢拉绳至轻环重新静止,此时QP段轻绳与天花板之间所夹的锐角为( )| A. | 90°-θ | B. | 45°-$\frac{θ}{2}$ | C. | 45°+$\frac{θ}{2}$ | D. | θ |
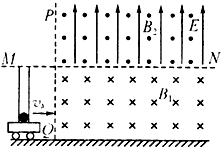 如图所示,水平地面上有一辆小车,车上固定一个竖直光滑绝缘管,管的底部有一质量m1=0.2g、电荷量q=8×10-5C的带正电小球,小球的直径比管的内径略小.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1=15T的匀强磁场,MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场,现让小车始终保持vx=2m/s的速度匀速向右运动,以带电小球刚经过磁场的边界PQ为计时的起点,测得小球在管内运动的这段时间为t=1s,g取10/s2,不计空气阻力.
如图所示,水平地面上有一辆小车,车上固定一个竖直光滑绝缘管,管的底部有一质量m1=0.2g、电荷量q=8×10-5C的带正电小球,小球的直径比管的内径略小.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1=15T的匀强磁场,MN面的上方还存在着竖直向上、场强E=25V/m的匀强电场和垂直纸面向外、磁感应强度B2=5T的匀强磁场,现让小车始终保持vx=2m/s的速度匀速向右运动,以带电小球刚经过磁场的边界PQ为计时的起点,测得小球在管内运动的这段时间为t=1s,g取10/s2,不计空气阻力.