题目内容
分)如图所示,空间存在着强度E=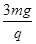 方向竖直向上的匀强电场,在电场内一长为
方向竖直向上的匀强电场,在电场内一长为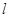 的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
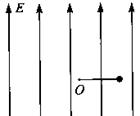
(1)小球运动最高点时的速度;
(2)细线能承受的最大拉力;
(3)从断线开始计时,在t=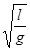 时刻小球与O点的距离。
时刻小球与O点的距离。
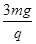 方向竖直向上的匀强电场,在电场内一长为
方向竖直向上的匀强电场,在电场内一长为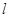 的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
(1)小球运动最高点时的速度;
(2)细线能承受的最大拉力;
(3)从断线开始计时,在t=
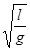 时刻小球与O点的距离。
时刻小球与O点的距离。 (1)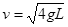 ;(2)6mg;(3)
;(2)6mg;(3)
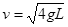 ;(2)6mg;(3)
;(2)6mg;(3)
试题分析:
(1)设小球运动到最高点时速度为v,只有重力和电场力做功,弹力不做功。对该过程由动能定理有,
 ① (2分)
① (2分)解得
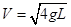 (1分)
(1分)(2)在最高点,小球受三个力作用,重力,电场力和细线的拉力,由向心力公式得,
 ②(2分)
②(2分)解得,T=6mg(1分)
(2)小球在细线断裂后,带电小球做类平抛运动,合力竖直向上的,在竖直方向的加速度设为a,则
 ③(2分)
③(2分)小球在t时刻
 (1分)
(1分) (1分)
(1分)小球与O点的距离
 (2分)
(2分)
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目

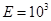 V/m,方向水平向左的匀强电场中,有一个小物块,质量为
V/m,方向水平向左的匀强电场中,有一个小物块,质量为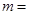 80g,带正电荷
80g,带正电荷 ,与水平轨道之间的动摩擦因数
,与水平轨道之间的动摩擦因数 0.2,在水平轨道的末端
0.2,在水平轨道的末端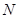 处,连接一个光滑的半圆形轨道,半径为
处,连接一个光滑的半圆形轨道,半径为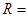 40cm,取
40cm,取 10m/s2,求:
10m/s2,求:
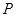 (轨道中点)点时对轨道的压力等于多少?
(轨道中点)点时对轨道的压力等于多少?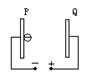


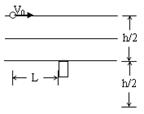
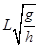
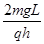
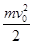
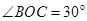 。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取
。可视为质点的小滑块从轨道AB上高H处的某点由静止滑下,用力传感器测出滑块经过圆轨道最高点D时对轨道的压力为F,并得到如图乙所示的压力F与高度H的关系图象,取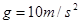 。求:
。求: