题目内容
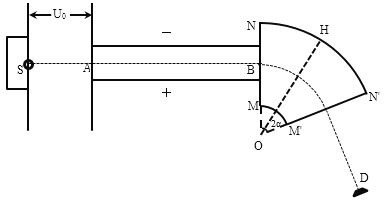
【题目】如图所示，在虚线PH的右侧是一条形匀强磁场，磁感应强度大小为B，方向垂直纸面向里。PH左侧是一宽度为d的条形匀强电场，场强大小为E，方向水平向左。在虚线PH上的一点O处有一静止的铀（
）核水平向左放出一个
粒子而衰变为钍（Th）核。已知元电荷电量为e，核子平均质量为m。设粒子与钍核分离后它们之间的作用力忽略不计，涉及动量问题时，亏损的质量可不计。
(1)写出铀核衰变方程；
(2)若粒子恰不离开电场区域，则磁场的宽度至少为多少，才能保证衰变生成物都不会离开磁场区域；
(3)在满足(2)的条件下，粒子和钍核先后经过PH上同一点N。求粒子和钍核从衰变到运动至N点的时间分别为多少。
【答案】(1)
； (2)
；（3）见解析。
【解析】
(1) 核反应过程质量数与核电荷数守恒，核反应方程式为
(2) 
粒子恰好不离开电场，对粒子，由动能定理得
解得
粒子在磁场中做圆周运动，由牛顿第二定律得
解得
发生衰变过程系统动量守恒，衰变后两粒子动量P大小相等、方向相反。
又
则有
只要粒子不出磁场，则钍核也不会离开磁场，则磁场的宽度至少为
(3)粒子与钍核衰变时动量等大反向，则有
则衰变后钍核的速度为
粒子在电场中匀减速运动的时间为
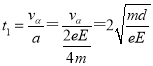
钍核在电场中减速运动的时间为
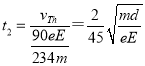
粒子在磁场中做匀速圆周运动的周期为
钍核在磁场中做匀速圆周运动的周期为
粒子从衰变到运动至N点时间为
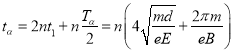
或
钍核粒子从衰变到运动至N点时间为
或
其中n=1，2，3……
练习册系列答案
相关题目
