题目内容
15.一质点沿直线Ox方向做变速运动,它离开O点的距离x随时间变化的关系为x=5+2t3(m),求该质点在t=0到t=2s这段时间内的平均速度大小和t=2s到t=3s这段时间内的平均速度的大小.分析 根据x=5+2t3(m),熟练写出相应时刻质点相对于原点o的位置坐标,根据位置坐标确定物体的位移大小,根据平均速度定义式直接得到相应时间内的平均速度.
解答 解:由题意一质点沿直线ox作加速运动,它离开O点的距离x随时间变化的关系为x=5+2t3(m),故可知:
t=0时刻,质点的位置坐标x0=5m,2s末的位置坐标x2=21m,3s末的位置坐标x3=59m
因为位移是质点位置坐标的变化量,故物体在前2s内的位移x0-2=x2-x0=16m,其平均速度$\overline{{v}_{1}}=\frac{{x}_{0-2}}{2}=\frac{16}{2}m/s=8m/s$
物体在第3s内的位移x2-3=x3-x2=38m,其平均速度$\overline{{v}_{2}}=\frac{{x}_{2-3}}{1}=\frac{38}{1}m/s=38m/s$
答:质点在t=0到t=2s间的平均速度大小为8m/s,从t=2s到t=3s间的平均速度大小为38m/s.
点评 熟练掌握位移为位置坐标的变化量,根据题目给出的表达式,求出相应时间末位移的位置坐标,从而求出其对应时间内的位移,根据平均速度求解即可.注意因为质点不是匀变速直线运动,故不能直接使用$\overline{v}=\frac{v+{v}_{0}}{2}$方法通过求对应时刻的速度来求平均速度.

练习册系列答案
相关题目
5.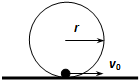 如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.5m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s2)( )
如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.5m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s2)( )
 如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.5m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s2)( )
如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.5m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s2)( )| A. | v0≤$\sqrt{10}$m/s | B. | v0≥5m/s | C. | v0≥2$\sqrt{5}$m/s | D. | v0≤2$\sqrt{2}$m/s |
3.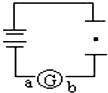 如图所示,将平行板电容器与电池组相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地增大距离,其他条件不变,则( )
如图所示,将平行板电容器与电池组相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地增大距离,其他条件不变,则( )
 如图所示,将平行板电容器与电池组相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地增大距离,其他条件不变,则( )
如图所示,将平行板电容器与电池组相连,两板间的带电尘埃恰好处于静止状态.若将两板缓慢地增大距离,其他条件不变,则( )| A. | 电容器带电量不变 | B. | 尘埃仍静止 | ||
| C. | 尘埃向下加速运动 | D. | 电容器带电量减小 |
7.如图1,倾角为 的光滑斜面与光滑的半圆形轨道光滑连接于B点,固定在水平面上,在半圆轨道的最高点C装有压力传感器,整个轨道处在竖直平面内,一小球自斜面上距底端高度为H的某点A由静止释放,到达半圆最高点C时,被压力传感器感应,通过与之相连的计算机处理,可得出小球对C点的压力F,改变H的大小,仍将小球由静止释放,到达C点时得到不同的F值,将对应的如图2F与H的值描绘在F-H图象中,如图所示,则下列说法不正确的是( )
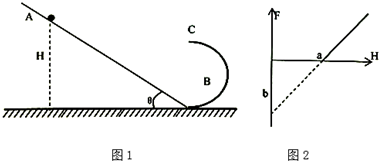

| A. | 图线的斜率与小球的质量无关 | |
| B. | b点坐标的绝对值与物块的质量成正比 | |
| C. | a的坐标与物块的质量无关 | |
| D. | 只改变斜面倾角,a、b两点的坐标均不变 |
4.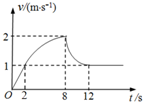 在某次消防演习中,一消防队员沿系在高处的一条悬垂的绳子由静止开始竖直滑下,经一段时间落地,运动的v-t图象如图所示,除2s~12s间的图线为曲线外,其它为直线.则下列关于消防队员的说法中正确的是( )
在某次消防演习中,一消防队员沿系在高处的一条悬垂的绳子由静止开始竖直滑下,经一段时间落地,运动的v-t图象如图所示,除2s~12s间的图线为曲线外,其它为直线.则下列关于消防队员的说法中正确的是( )
 在某次消防演习中,一消防队员沿系在高处的一条悬垂的绳子由静止开始竖直滑下,经一段时间落地,运动的v-t图象如图所示,除2s~12s间的图线为曲线外,其它为直线.则下列关于消防队员的说法中正确的是( )
在某次消防演习中,一消防队员沿系在高处的一条悬垂的绳子由静止开始竖直滑下,经一段时间落地,运动的v-t图象如图所示,除2s~12s间的图线为曲线外,其它为直线.则下列关于消防队员的说法中正确的是( )| A. | 0~8s内处于超重状态,8s~12s处于失重状态 | |
| B. | 0~8s内做加速度逐渐减小的加速运动 | |
| C. | 2~8s内的平均速度等于8s~12s内的平均速度 | |
| D. | 0~8s的平均加速度不等于8s~12s的平均加速度 |

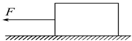 如图所示,静止在水平面上的物体,所受重力为200N,物体和水平面之间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力大小.求下列两种情况中的摩擦力:
如图所示,静止在水平面上的物体,所受重力为200N,物体和水平面之间的动摩擦因数μ=0.1,最大静摩擦力等于滑动摩擦力大小.求下列两种情况中的摩擦力: