题目内容
5.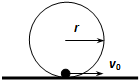 如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.5m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s2)( )
如图所示,竖直放置的光滑圆轨道被固定在水平地面上,半径r=0.5m,最低点处有一小球(半径比r小很多),现给小球以水平向右的初速度v0,则要使小球不脱离圆轨道运动,v0应当满足(g=10m/s2)( )| A. | v0≤m/s | B. | v0≥5m/s | C. | v0≥2m/s | D. | v0≤2m/s |
分析 要使小球不脱离轨道运动,1、越过最高点.2、不越过四分之一圆周.再根据机械能守恒定律求出初速度v0的条件
解答 解:最高点的临界情况:mg=m,
解得:v=
根据机械能守恒定律得:-mg•2r=mv2-mv02
解得:v0=5m/s.
若不通过四分之一圆周,根据动能定理有:
-mgr=0-mv02
解得:v0=m/s.
所以初速度v0范围为v0≥5m/s或v0≤m/s.故AB正确,CD错误.
故选:AB
点评 解决本题的关键知道小球在内轨道运动最高点的临界情况,以及能够熟练运用机械能守恒定律,明确机械能守恒的条件的应用.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
15.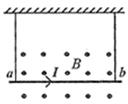 如图所示,金属棒以用软导线悬挂在磁感应强度为B,方向垂直纸面向外的匀强磁场中,ab通以如图所示的电流I,此时悬线有一定的张力,若要使悬线张力为零,下列做法中有可能实现的是( )
如图所示,金属棒以用软导线悬挂在磁感应强度为B,方向垂直纸面向外的匀强磁场中,ab通以如图所示的电流I,此时悬线有一定的张力,若要使悬线张力为零,下列做法中有可能实现的是( )
 如图所示,金属棒以用软导线悬挂在磁感应强度为B,方向垂直纸面向外的匀强磁场中,ab通以如图所示的电流I,此时悬线有一定的张力,若要使悬线张力为零,下列做法中有可能实现的是( )
如图所示,金属棒以用软导线悬挂在磁感应强度为B,方向垂直纸面向外的匀强磁场中,ab通以如图所示的电流I,此时悬线有一定的张力,若要使悬线张力为零,下列做法中有可能实现的是( )| A. | 增大磁感应强度B | B. | 增大ab中的电流I | ||
| C. | 改变电流I的方向 | D. | 改变磁感应强度B的方向 |
16.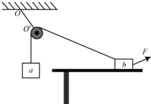 如图所示,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图所示,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
 如图所示,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )
如图所示,一光滑的轻滑轮用细绳OO'悬挂于O点;另一细绳跨过滑轮,其一端悬挂物块a,另一端系一位于水平粗糙桌面上的物块b.外力F向右上方拉b,整个系统处于静止状态.若F方向不变,大小在一定范围内变化,物块b仍始终保持静止,则( )| A. | 物块b所受到的支持力也在一定范围内变化 | |
| B. | 绳OO'的张力也在一定范围内变化 | |
| C. | 连接a和b的绳的张力也在一定范围内变化 | |
| D. | 物块b与桌面间的摩擦力也在一定范围内变化 |
20. 在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )
在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )
 在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )
在研究一个微型电动机的性能时,应用了图示的试验电路.闭合开关,当调节变阻器R使电动机停止转动时,电流表和电压表的示数分别为0.5A和2V;再调节R使电动机正常运转时,电流表和电压表的示数分别为2A和24V.则这个电动机正常运转时的输出功率为( )| A. | 48w | B. | 47w | C. | 32w | D. | 44w |
17.下列说法正确的是( )
| A. | 研究跳水运动员的姿势时运动员可以看成质点 | |
| B. | 讨论火车从某一路标经过的时间时火车可以看成质点 | |
| C. | 讨论某同学从贵龙中学骑自行车到丁字口的时间,该自行车能看成质点 | |
| D. | ”天宫一号”与“神舟一号”对接时“神州一号”能看成质点 |
14.为了防止静电危害,应尽快把静电导走,下面的措施中不是利用静电知识防止危害的有( )
| A. | 油罐车后面装一条拖地铁链 | B. | 电工钳柄上套有一绝缘套 | ||
| C. | 飞机轮胎用导电橡胶制成 | D. | 印染车间保持适当的湿度 |

 如图所示,半径R=4.85m的四分之一光滑圆轨道固定于地面上,在地面上紧靠轨道依次排放两块木板A、B,质量均为m2=20kg,木板上表面与圆轨道末端相切,物块与木板间的动摩擦因数均为μ1=0.4,木板A与地面间的动摩擦因数μ2=0.2,A的长度为l=2m,B与地面间的动摩擦因数为零,在离B右端很远的地方有一弹性装置C.将质量为m1=10kg的物块(可视为质点)从轨道顶端无初速滑下,物块滑过A后滑上B,若B与C、A碰撞后B的速度大小不变,方向相反;B在A、C间做往复运动时,每次碰前物块与B已达到共速.(设最大静摩擦力与滑动摩擦力大小相等,取g=10m/s2).
如图所示,半径R=4.85m的四分之一光滑圆轨道固定于地面上,在地面上紧靠轨道依次排放两块木板A、B,质量均为m2=20kg,木板上表面与圆轨道末端相切,物块与木板间的动摩擦因数均为μ1=0.4,木板A与地面间的动摩擦因数μ2=0.2,A的长度为l=2m,B与地面间的动摩擦因数为零,在离B右端很远的地方有一弹性装置C.将质量为m1=10kg的物块(可视为质点)从轨道顶端无初速滑下,物块滑过A后滑上B,若B与C、A碰撞后B的速度大小不变,方向相反;B在A、C间做往复运动时,每次碰前物块与B已达到共速.(设最大静摩擦力与滑动摩擦力大小相等,取g=10m/s2).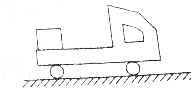 如图所示,一辆汽车在平直公路上,车上有一木箱,试判断下列情况中,木箱所受摩擦力的方向,以及此摩擦力是动力还是阻力.
如图所示,一辆汽车在平直公路上,车上有一木箱,试判断下列情况中,木箱所受摩擦力的方向,以及此摩擦力是动力还是阻力.