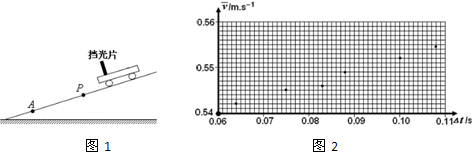
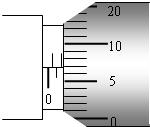
题目内容
5.如图甲所示,物块A与质量为m的小球B通过不可伸长的轻质细绳跨过两等高定滑轮连接.物块A置于左侧滑轮正下方的表面水平的压力传感装置上,小球与右侧滑轮的距离为l0开始时物块和小球均静止,将此时传感装置的示数记为N1.现给小球施加水平力F,将小球缓慢拉起至细绳与竖直方向成53°角,如图乙所示,此时传感装置的示数记为N2,已知N1:N2=9:7;再将小球由静止释放,当小球B运动至最低位置时,传感装置的示数与刚释放时恰好相同,不计滑轮的大小和摩擦,重力加速度的大小为g.求:
(1)物块A的质量M与小球B的质量m之比:
(2)从释放到运动至最低位置的过程中,小球克服阻力所做的功;
(3)若小球释放后忽略阻力的影响,小球运动到最低点时传感装置的示数N3

分析 (1)分别对开始及夹角为530时进行受力分析,由共点力平衡列式,联立可求得物块A的质量M与小球B的质量m之比;
(2)对最低点由向心力公式进行分析求解物块的速度,再对全过程由动能定理列式,联立可求得克服阻力做功;
(3)无空气阻力时,由动能定理和牛顿第二定律列式联立可求小球运动到最低点时传感装置的示数.
解答 解:(1)初始时:N1=Mg-mg
F作用,在530时,绳中拉力为:T1=$\frac{mg}{cos5{3}^{0}}$=$\frac{5}{3}$mg
此时:N2=Mg-T1,又:$\frac{{N}_{1}}{{N}_{2}}$=$\frac{9}{7}$
联立解得:M:m=4:1
(2)从释放到最低点,由动能定理:Mg(1-cos53°)-Wf=$\frac{1}{2}$mv2-0
在最低点:N2-mg=m$\frac{{v}^{2}}{l}$
联立解得:Wf=$\frac{1}{15}$mgl
(3)无空气阻力时,由动能定理:mgl(1-cos53°)=$\frac{1}{2}$mv12-0
在最低点:T2-mg=m$\frac{{v}_{1}^{2}}{l}$
联立解得:T2=$\frac{9}{5}$mg
所以传感装置的示数为:N3=Mg-T2=2.2mg.
答:(1)物块A的质量M与小球B的质量m之比为4:1;
(2)从释放到运动至最低位置的过程中,小球克服阻力所做的功为$\frac{1}{15}$mgl;
(3)小球运动到最低点时传感装置的示数为2.2mg.
点评 本题考查动能定理及共点力的平衡条件的应用,要注意正确选择研究对象,做好受力分析及过程分析;进而选择正确的物理规律求解;要注意在学习中要对多个方程联立求解的方法多加训练.

练习册系列答案
相关题目
16.下列说法正确的是( )
| A. | 牛顿根据理想斜槽实验得出了惯性定律 | |
| B. | v=$\frac{△x}{△t}$、B=$\frac{F}{IL}$、a=$\frac{F}{m}$ 均采用了比值定义法 | |
| C. | 亚里士多德的观点是力是改变物体运动状态的原因 | |
| D. | 把曲线运动分解为直线运动来处理应用了等效替代法 |
13. 如图所示,其中电流表 A 的量程为 0.6A,表盘均匀划分为 30 个小格,每小格表示 0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2 的阻值等于电流表内阻的 2 倍,若用电流表 A 的表盘刻度表示流过接线柱 1 的电流值,则下列分析正确的是( )
如图所示,其中电流表 A 的量程为 0.6A,表盘均匀划分为 30 个小格,每小格表示 0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2 的阻值等于电流表内阻的 2 倍,若用电流表 A 的表盘刻度表示流过接线柱 1 的电流值,则下列分析正确的是( )
 如图所示,其中电流表 A 的量程为 0.6A,表盘均匀划分为 30 个小格,每小格表示 0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2 的阻值等于电流表内阻的 2 倍,若用电流表 A 的表盘刻度表示流过接线柱 1 的电流值,则下列分析正确的是( )
如图所示,其中电流表 A 的量程为 0.6A,表盘均匀划分为 30 个小格,每小格表示 0.02A;R1的阻值等于电流表内阻的$\frac{1}{2}$;R2 的阻值等于电流表内阻的 2 倍,若用电流表 A 的表盘刻度表示流过接线柱 1 的电流值,则下列分析正确的是( )| A. | 将接线柱 1、2 接入电路时,每一小格表示 0.04A | |
| B. | 将接线柱 1、2 接入电路时,每一小格表示 0.02A | |
| C. | 将接线柱 1、3 接入电路时,每一小格表示 0.06A | |
| D. | 将接线柱 1、3 接入电路时,每一小格表示 0.01A |
17.在下面研究的各个问题中可以被看作质点的是( )
| A. | 研究奥运会乒乓球男单冠军孔令辉打出的弧旋球 | |
| B. | 考查奥运会冠军王军霞在万米长跑中的速度 | |
| C. | 观察跳水冠军伏明霞在跳水比赛中的动作 | |
| D. | 研究一列火车通过某一路标的时间 |
3. 如图所示,沿水平方向放置的平行金属板a和b,分别与电源的正、负极相连,两板的中央沿竖直方向各有一个小孔,一带正电的液滴,自小孔的正上方的P点由静止自由落下,开关S闭合时,穿过a板的小孔后的速度为v1.若使b板不动,保持开关S闭合或断开,a板向下平移一小段距离,相同的液滴仍然从P点由静止自由落下,穿过a板的小孔后的速度为v2,不计空气阻力,下列说法正确的是( )
如图所示,沿水平方向放置的平行金属板a和b,分别与电源的正、负极相连,两板的中央沿竖直方向各有一个小孔,一带正电的液滴,自小孔的正上方的P点由静止自由落下,开关S闭合时,穿过a板的小孔后的速度为v1.若使b板不动,保持开关S闭合或断开,a板向下平移一小段距离,相同的液滴仍然从P点由静止自由落下,穿过a板的小孔后的速度为v2,不计空气阻力,下列说法正确的是( )
 如图所示,沿水平方向放置的平行金属板a和b,分别与电源的正、负极相连,两板的中央沿竖直方向各有一个小孔,一带正电的液滴,自小孔的正上方的P点由静止自由落下,开关S闭合时,穿过a板的小孔后的速度为v1.若使b板不动,保持开关S闭合或断开,a板向下平移一小段距离,相同的液滴仍然从P点由静止自由落下,穿过a板的小孔后的速度为v2,不计空气阻力,下列说法正确的是( )
如图所示,沿水平方向放置的平行金属板a和b,分别与电源的正、负极相连,两板的中央沿竖直方向各有一个小孔,一带正电的液滴,自小孔的正上方的P点由静止自由落下,开关S闭合时,穿过a板的小孔后的速度为v1.若使b板不动,保持开关S闭合或断开,a板向下平移一小段距离,相同的液滴仍然从P点由静止自由落下,穿过a板的小孔后的速度为v2,不计空气阻力,下列说法正确的是( )| A. | 若开关S保持闭合,向下移动a板,则v2>v1 | |
| B. | 若开关S保持闭合,向下移动a板,则金属板间的电场强度增大 | |
| C. | 若开关S闭合一段时间后再断开,向下移动a板,则v2一定等于v1 | |
| D. | 若开关S闭合一段时间后再断开,向下移动a板,则金属板间的电场强度不变 |
 在如图所示的电路中,电源的电动势E=3.6V,内电阻r=0.6Ω,外电路的电阻R=3.0Ω.闭合开关S.求:
在如图所示的电路中,电源的电动势E=3.6V,内电阻r=0.6Ω,外电路的电阻R=3.0Ω.闭合开关S.求: