题目内容
16.两个质量和电荷量均相同的带电粒子a、b分别以速度v和2v垂直射入一匀强磁场,其轨道半径分别为ra和rb,运动的周期为Ta和Tb.不计粒子重力,则( )| A. | ra>rb | B. | ra<rb | C. | Ta>Tb | D. | Ta<Tb |
分析 由牛顿第二定律研究轨道半径,由周期T=$\frac{2πr}{v}$=$\frac{2πm}{Bq}$分析周期大小.
解答 解:AB、根据牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$得:r=$\frac{mv}{qB}$,由题m、q、B大小均相同,速度大的半径大,故ra<rb,故A错误,B正确;
CD、周期T=$\frac{2πr}{v}$=$\frac{2πm}{Bq}$,知由题m、q、B大小均相同,周期相同,故CD错误;
故选:B
点评 此题关键知带电粒子在磁场中是洛伦兹力充当向心力,列式得到要求的物理量从而比较大小.

练习册系列答案
相关题目
7.两个相同的金属小球分别带有正、负电荷,固定在一定的距离上,现在把它们相接触后放回原处,则它们之间的库仑力的大小与原来相比将( )
| A. | 一定变小 | B. | 可能变大 | C. | 可能不变 | D. | 一定变大 |
11.已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发态跃迁的说法中正确的是( )
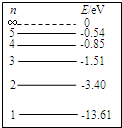
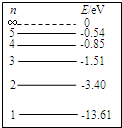
| A. | 一个具有Ek0=13.60eV动态,处于基态的氢原子和一个静止的同样处于基态的氢原子发生对心碰撞,可能跃迁到n=2能级的第一激发态 | |
| B. | 一个具有Ek0=13.60eV动态,处于基态的氢原子与一个静止的同样处于基态的氢原子发生对心碰撞,原子不可能跃迁到其他激发态 | |
| C. | 用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子能跃迁到n=2能级的轨道上去 | |
| D. | 用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子不能跃迁到其他轨道上去 | |
| E. | 用动能为12.3eV的电子去射向一群处于基态的氢原子,氢原子受电子照射后,原子能跃迁到n=2能级的轨道上去 |
1.关于电磁打点计时器的使用,下列说法正确的是( )
| A. | 电磁打点计时器使用的是6V左右的直流电源 | |
| B. | 在测量物体速度时,先让物体运动,后接通电源 | |
| C. | 使用的电源频率越高,打点的时间间隔就越大 | |
| D. | 在同一纸带上打的点越密,说明物体运动的速度越慢 |
8.“天宫一号”是中国首个空间站的名称,已知“天宫一号”目标飞行器属于近地轨道卫星,比地球同步卫星的轨道半径小得多,设“天宫一号”和同步卫星运行的线速度分别为v1和v2,运行周期分别为T1和 T2,下列说法正确的是( )
| A. | v1>v2,T1>T2 | B. | v1<v2,T1<T2 | C. | v1>v2,T1<T2 | D. | v1<v2,T1>T2 |
6.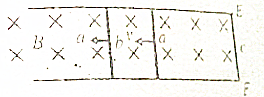 如图所示,磁感应强度为B的匀强磁场中,三根相同的金属棒a,b,c,其中c固定在相距为L的平行金属导轨的右端,a,b以相同的速度v沿导轨运动,则:( )
如图所示,磁感应强度为B的匀强磁场中,三根相同的金属棒a,b,c,其中c固定在相距为L的平行金属导轨的右端,a,b以相同的速度v沿导轨运动,则:( )
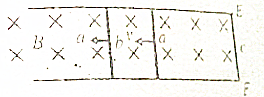 如图所示,磁感应强度为B的匀强磁场中,三根相同的金属棒a,b,c,其中c固定在相距为L的平行金属导轨的右端,a,b以相同的速度v沿导轨运动,则:( )
如图所示,磁感应强度为B的匀强磁场中,三根相同的金属棒a,b,c,其中c固定在相距为L的平行金属导轨的右端,a,b以相同的速度v沿导轨运动,则:( )| A. | c两端的电压为BLv | |
| B. | c两端的电压为$\frac{1}{2}$BLv | |
| C. | 流过c的电流方向为E→c→F | |
| D. | 流过a,b,c的电流之比为Ia:Ib:Ic=1:1:2 |
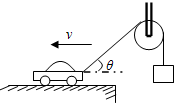 如图,在水平路面上行使的汽车,通过光滑定滑轮吊着一重物,当汽车水平向左匀速行驶时,重物向上做加速运动(填“加速”或“减速”),若汽车速度为6m/s,某时刻轻绳与水平方向的夹角θ为60°时,物体上升的速度大小为3m/s.
如图,在水平路面上行使的汽车,通过光滑定滑轮吊着一重物,当汽车水平向左匀速行驶时,重物向上做加速运动(填“加速”或“减速”),若汽车速度为6m/s,某时刻轻绳与水平方向的夹角θ为60°时,物体上升的速度大小为3m/s.