题目内容
11.已知氢原子的能级图如图所示,则下列有关处于基态的氢原子向激发态跃迁的说法中正确的是( )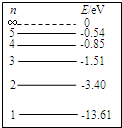
| A. | 一个具有Ek0=13.60eV动态,处于基态的氢原子和一个静止的同样处于基态的氢原子发生对心碰撞,可能跃迁到n=2能级的第一激发态 | |
| B. | 一个具有Ek0=13.60eV动态,处于基态的氢原子与一个静止的同样处于基态的氢原子发生对心碰撞,原子不可能跃迁到其他激发态 | |
| C. | 用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子能跃迁到n=2能级的轨道上去 | |
| D. | 用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子不能跃迁到其他轨道上去 | |
| E. | 用动能为12.3eV的电子去射向一群处于基态的氢原子,氢原子受电子照射后,原子能跃迁到n=2能级的轨道上去 |
分析 根据碰撞过程中的动量守恒与能量守恒求解碰撞前运动氢原子的最小动能,与给出的原子的动能比较即可;吸收光子能量发生跃迁,吸收的光子能量需等于两能级间的能级差;根据电子的碰撞,光子可以获取10.2eV能量,从而发生跃迁.
解答 解:AB、要使运动氢原子的速度最小,则必须使二氢原子发生正碰时氢原子发生完全非弹性碰撞损失的动能将全部被基态氢原子所吸收,
由玻尔理论知二基态氢原子碰撞时损失的动能的最小值必为氢原子从n=1激发到n=2能级的能量差△E=E2-E1=(-3.4)-(-13.6)=10.2eV ①
设碰前运动的氢原子最小速度为v0,初动能为Ek,碰后二氢原子速度为v,
由动量守恒得mv0=2mv,②
由能量守恒得:$\frac{1}{2}$m${v}_{0}^{2}$=$\frac{1}{2}$•2mv2+△E ③
$\frac{1}{2}$m${v}_{0}^{2}$=E0 ④
代入数据得:E0=20.4eV>13.6eV
所以不能使基态氢原子发生能级跃迁,故A错误,B正确;
CD、吸收光子能量发生跃迁,吸收的光子能量需等于两能级间的能级差,即△E=E2-E1=(-3.4)-(-13.6)=10.2eV,
因此用能量为12.3eV的光子去照射一群处于基态的氢原子,受光子照射后,原子不能跃迁到其他轨道上去,故C错误,D正确;
E、当用动能为12.3eV的电子去射向一群处于基态的氢原子,氢原子受电子照射后,原子可能吸收10.2eV的能量,从而使得原子能跃迁到n=2能级的轨道上去,故E正确;
故选:BDE.
点评 解决本题的关键知道能级差与吸收或辐射光子能量的关系,即Em-En=hv.并掌握碰撞中的动量守恒定律与能量守恒,注意用光子照射与电子碰撞,产生的不同情况.

练习册系列答案
相关题目
1.降落伞在匀速下降过程中遇到水平方向吹来的风,若风速越大,则降落伞( )
| A. | 落地时速度越小 | B. | 落地时速度越大 | C. | 下落的时间越短 | D. | 下落的时间越长 |
6.振动周期为T、振幅为A、位于x=0点的波源从平衡位置沿y轴正向开始做简谐运动.该波源产生的一维简谐横波沿x轴正向传播,波速为v,传播过程中无能量损失.一段时间后,该振动传播至某质点P,关于质点P振动的说法正确的是( )
| A. | 振幅一定为A | |
| B. | 速度的最大值一定为v | |
| C. | 开始振动的方向沿y轴向上或向下取决于它离波源的距离 | |
| D. | 若P点与波源距离s=vT,则质点P的位移与波源的相同 |
16.两个质量和电荷量均相同的带电粒子a、b分别以速度v和2v垂直射入一匀强磁场,其轨道半径分别为ra和rb,运动的周期为Ta和Tb.不计粒子重力,则( )
| A. | ra>rb | B. | ra<rb | C. | Ta>Tb | D. | Ta<Tb |
3.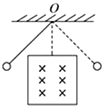 如图所示的圆形导体环用一根轻质细杆悬挂在O点,导体环可以在竖直平面里来回摆动,空气阻力和摩擦力均可不计.在如图所示的正方形区域里,有匀强磁场垂直于圆环的振动面指向纸内.下列说法中错误的是( )
如图所示的圆形导体环用一根轻质细杆悬挂在O点,导体环可以在竖直平面里来回摆动,空气阻力和摩擦力均可不计.在如图所示的正方形区域里,有匀强磁场垂直于圆环的振动面指向纸内.下列说法中错误的是( )
 如图所示的圆形导体环用一根轻质细杆悬挂在O点,导体环可以在竖直平面里来回摆动,空气阻力和摩擦力均可不计.在如图所示的正方形区域里,有匀强磁场垂直于圆环的振动面指向纸内.下列说法中错误的是( )
如图所示的圆形导体环用一根轻质细杆悬挂在O点,导体环可以在竖直平面里来回摆动,空气阻力和摩擦力均可不计.在如图所示的正方形区域里,有匀强磁场垂直于圆环的振动面指向纸内.下列说法中错误的是( )| A. | 此摆振动的开始阶段机械能不守恒 | |
| B. | 导体环进入磁场和离开磁场时,环中电流的方向肯定相反 | |
| C. | 导体环通过最低点时,环中感应电流最大 | |
| D. | 最后此摆在匀强磁场中振动时,机械能守恒 |
20.下列说法正确的是( )
| A. | 万有引力定律揭示了宇宙中有质量的物体间普遍存在着一种相互吸引力 | |
| B. | 万有引力的大小跟一个物体的质量成正比,也跟相互作用的另一个物体的质量成正比 | |
| C. | 某两位同学相距较近时,却没有感觉到对方的吸引力,那是因为万有引力定律只适用于较大物体间的作用 | |
| D. | 万有引力定律公式中的G是常数,是牛顿通过实验测出的 |
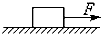 如图所示,质量为2kg的物体静止在水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等,t=0时,物体受到方向不变的水平拉力F的作用,F的大小在不同时间段内有不同的值,具体情况如表格所示,g取10m/s2,求3s末拉力F的瞬时功率.
如图所示,质量为2kg的物体静止在水平地面上,物体与地面间的动摩擦因数为0.2,最大静摩擦力与滑动摩擦力大小视为相等,t=0时,物体受到方向不变的水平拉力F的作用,F的大小在不同时间段内有不同的值,具体情况如表格所示,g取10m/s2,求3s末拉力F的瞬时功率.