题目内容
【题目】在竖直墙壁的左侧水平地面上,放置一个质量为M的正方体ABCD,在墙壁和正方体之间放置一半径为R、质量为m的光滑球,正方体和球均保持静止,如图所示。球的球心为O,OB与竖直方向的夹角为![]() ,正方体与水平地面的动摩擦因数为
,正方体与水平地面的动摩擦因数为![]() 。(g已知,并取最大静摩擦力等于滑动摩擦力)求:
。(g已知,并取最大静摩擦力等于滑动摩擦力)求:
(1)正方体和墙壁对球的支持力F1、F2分别是多大?
(2)若![]() =45°,保持正方体的质量M不变,增大球的质量,为了不让正方体出现滑动,则球的质量最大为多少?(
=45°,保持正方体的质量M不变,增大球的质量,为了不让正方体出现滑动,则球的质量最大为多少?(![]() )
)
(3)若球的质量![]() ,改变正方体到墙壁之间的距离,要使正方体不出现滑动, 则正方体的右侧面AB到墙壁的最大距离是多少?
,改变正方体到墙壁之间的距离,要使正方体不出现滑动, 则正方体的右侧面AB到墙壁的最大距离是多少?

【答案】(1)![]() ,N 2=mgtan
,N 2=mgtan![]() ;(2)m<
;(2)m<![]() ;(3)
;(3)![]() R。
R。
【解析】
(1)对球受力情况如图所示
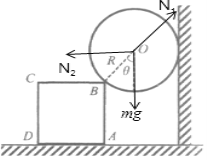
根据平衡条件知:
N1cosθ=mg
N1sinθ=N2
解得
![]()
N2=mgtanθ
(2)对整体受力分析
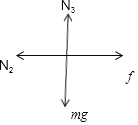
根据平衡条件知:
N3=Mg+mg
N2=f
f≤μN3
三式联立
mgtanθ≤μ(Mg+mg)①
解得
![]()
(3)设与竖直方向夹角为α,根据①式知
![]()
解得
tanα=![]()
即
α=60°
则正方形到墙距离为
d=Rsin60°+R=![]() R
R

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目