题目内容
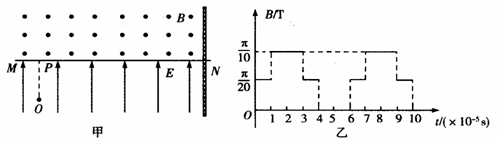
(20分)如图甲所示,两平行金属板长度l不超过0.2 m,两板间电压U随时间t变化的图象如图乙所示。在金属板右侧有一左边界为MN、右边无界的匀强磁场,磁感应强度B =0.01 T,方向垂直纸面向里。现有带正电的粒子连续不断地以速度v0=105m/s射入电场中,初速度方向沿两板间的中线OO’方向。磁场边界MN与中线OO’垂直。已知带电粒子的比荷q/m=108C/kg,粒子的重力和粒子之间的相互作用力均可忽略不计。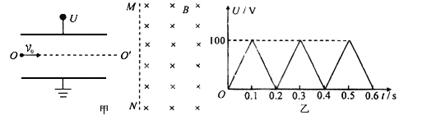
(1)在每个粒子通过电场区域的时间内,可以把板间的电场强度看作是恒定的。请通过计算说明这种处理能够成立的理由;
(2)设t=0.1 s时刻射人电场的带电粒子恰能从金属板边缘穿越电场射入磁场,求该带电粒子射出电场时速度的大小;
(3)对于所有经过电场射入磁场的带电粒子,设其射人磁场的入射点和从磁场射出的出射点间的距离为d,试判断d的大小是否随时间变化?若不变,证明你的结论;若变化,求出d的变化范围。
(1)见解析(2)1.41×105m/s (3)d= 不随时间而变化
不随时间而变化
解析试题分析:(1)带电粒子在金属板间运动时间t= ,T=0.2 s
,T=0.2 s
得t<<T,(或t时间内金属板间电压变化ΔU≤2×10-3 V,变化很小)
故t时间内金属板间的电场可以认为是恒定的
(2)t=0.1 s时刻偏转电压U=100 V
带电粒子沿两板间的中线射入电场恰从平行金属板边缘飞出电场,电场力做功W=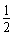 qU
qU
由动能定理:W=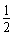 mv12-
mv12-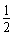 mv02
mv02
代入数据可得v1=1.41×105m/s
(3)设某一任意时刻射出电场的粒子速率为v,速度方向与水平方向的夹角为α,则 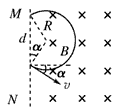
v=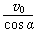
粒子在磁场中有qvB=m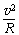
可得粒子进入磁场后,在磁场中做圆周运动的半径R=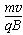
由几何关系d=2Rcosα
可得:d= =0.2 m,故d不随时间而变化
=0.2 m,故d不随时间而变化
考点:带电粒子在电场磁场中的运动、动能定理、牛顿定律等。

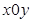 内,有一质量为
内,有一质量为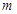 ,电荷量为
,电荷量为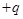 的粒子A从原点O沿y 轴正方向以初速度
的粒子A从原点O沿y 轴正方向以初速度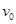 射出,粒子重力忽略不计,现要求该粒子能通过点P(a, -b),可通过在粒子运动的空间范围内加适当的“场”实现。
射出,粒子重力忽略不计,现要求该粒子能通过点P(a, -b),可通过在粒子运动的空间范围内加适当的“场”实现。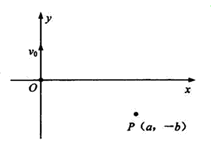
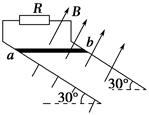
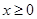 的区域内有垂直于xOy坐标平面向外的匀强磁场,X轴上A点坐标为(-L,0),Y轴上B点的坐标为(0,
的区域内有垂直于xOy坐标平面向外的匀强磁场,X轴上A点坐标为(-L,0),Y轴上B点的坐标为(0,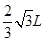 )。有一个带正电的粒子从A点以初速度vA沿y轴正方向射入匀强电场区域,经过B点进入匀强磁场区域,然后经x轴上的C点 (图中未画出)运动到坐标原点O。不计重力。求:
)。有一个带正电的粒子从A点以初速度vA沿y轴正方向射入匀强电场区域,经过B点进入匀强磁场区域,然后经x轴上的C点 (图中未画出)运动到坐标原点O。不计重力。求:

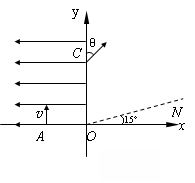
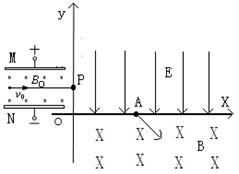
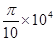 N/C。现将一重力不计、比荷
N/C。现将一重力不计、比荷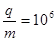 C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。
C/kg的正电荷从电场中的O点由静止释放,经过t0=1×10-5s后,通过MN上的P点进入其上方的匀强磁场。磁场方向垂直于纸面向外,以电荷第一次通过MN时开始计时,磁感应强度按图乙所示规律周期性变化。