题目内容
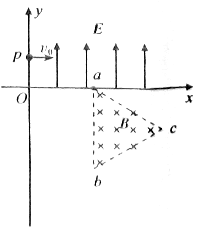
如图甲所示,建立x0y坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为L,第Ⅰ、Ⅳ象限分布着匀强磁场,方向垂直于x0y平面向里。位于极板左侧的粒子源可沿x轴向右发射质量为m、电量为q、速度相同、重力不计的带正电粒子。在0~3t0时间内两极板所加电压如图乙所示。已知,若粒子在t=0时刻射入,将恰好在t0时刻经极板边缘射入磁场。上述m、q、L、t0为已知量,且忽略粒子间的相互影响。求:
(1)电压U0的大小;
(2)匀强磁场的磁感应强度B;
(3)0~3t0时间内何时射入的粒子在磁场中运动的时间最短,并求出此最短时间。
(1) (2)
(2)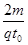 (3)
(3)
解析试题分析:(1)根据t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射出,则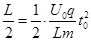 解得
解得 。
。
(2)水平方向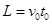 ,竖直方向
,竖直方向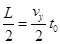 ;解得
;解得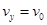 则
则 ,
,
所以速度偏转角为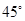 ,
,
由几何关系可知 ,
,
由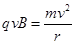
得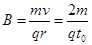 。
。
(3) 时刻进入两板间的带电粒子(运动轨迹如图)在磁场中的运动时间最短。
时刻进入两板间的带电粒子(运动轨迹如图)在磁场中的运动时间最短。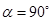


考点:此题考查带电粒子在电场中的偏转和在磁场中的圆周运动。

练习册系列答案
相关题目
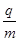 =106 C/kg的正电荷置于电场中的O点由静止释放,经过
=106 C/kg的正电荷置于电场中的O点由静止释放,经过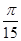 ×10-5 s后,电荷以v0=1.5×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求:
×10-5 s后,电荷以v0=1.5×104 m/s的速度通过MN进入其上方的匀强磁场,磁场与纸面垂直,磁感应强度B按图b所示规律周期性变化(图b中磁场以垂直纸面向外为正,以电荷第一次通过MN时为t=0时刻).求: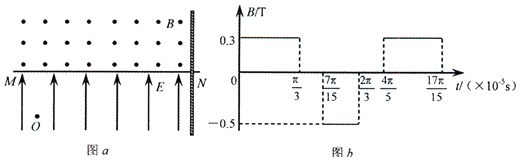
 ×10-5 s时刻电荷与O点的水平距离;
×10-5 s时刻电荷与O点的水平距离;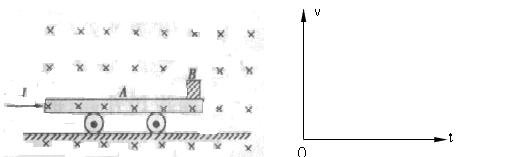


 点.若在直角坐标系xOy的第一象限区域内,加上方向沿y轴正方向、大小为E=Bv0的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q.忽略电子间的相互作用,不计电子的重力.试求:
点.若在直角坐标系xOy的第一象限区域内,加上方向沿y轴正方向、大小为E=Bv0的匀强电场,在x=3a处垂直于x轴放置一平面荧光屏,与x轴交点为Q.忽略电子间的相互作用,不计电子的重力.试求: