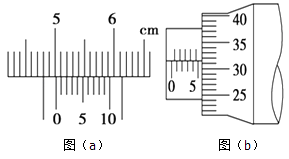
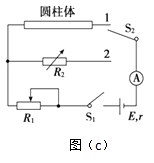
��Ŀ����
����Ŀ���ϰ������ϸ˺��ϰ�ͷ���ɵIJ��ع��ߣ���ͼ�������ϰ�ͷ������Ϊm���ϸ��������Ժ��ԣ��ϰ�ͷ��ذ�֮��Ķ�Ħ������Ϊ���������������ٶ�Ϊg��ijͬѧ�ø��ϰ���ˮƽ�ذ����ϵ�ʱ�����ϸ˷������ϰѣ��ϸ�����ֱ����ļн�Ϊ����
��1�����ϰ�ͷ�ڵذ��������ƶ��������ϰѵ����Ĵ�С��
��2������ʹ���ϰ��ڵذ��ϴӾ�ֹ�պÿ�ʼ�˶���ˮƽ�������ʱ�ذ���ϰѵ���ѹ���ı�ֵΪ������֪����һ�ٽ����0�����ȡܦ�0�������ϸ˷�����������������ʹ�ϰѴӾ�ֹ��ʼ�˶�������һ�ٽ�ǵ�����tan��0��

���𰸡���1��![]() ; ��2��
; ��2��![]()
�������������������1�����ͬѧ���ϸ˷����ô�СΪF�������ϰѣ������ϰѵ�������ֱ��ˮƽ����ֽ⣬��ƽ�������ã� ![]() ��
��
![]() ��
��
ʽ��![]() ��
��![]() �ֱ�Ϊ�ذ���ϰѵ���ѹ����Ħ��������
�ֱ�Ϊ�ذ���ϰѵ���ѹ����Ħ��������
![]() ��
��
�����٢ڢ�ʽ��![]() ��
��
��2��ʹ���ϰ��ڵذ��ϴӾ�ֹ�պÿ�ʼ�˶���ˮƽ���������ϰ���ذ������Ħ��������Ϊ![]() �����������У�
������������ ![]() ��
��
���������ϸ˷����ö�����������ʹ�ϰѴӾ�ֹ��ʼ�˶���Ӧ����
![]() ��
��
![]() ��
��
�����ݢޢ�ʽ��![]() ��
��
��Ϊ��ʽ�ұ���mg���Ǵ����㣬Ҫʹ��FΪ����ֵʱ��ʽ���dz�����ֻҪ����![]() ��
��
����![]() ��
��
��ʽȡ�Ⱥż�Ϊ�ٽ�״̬����![]()

 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�