题目内容
【题目】如图所示,质量为m的小球,用OB和O′B两根轻绳吊着,两轻绳与水平天花板的夹角分别为30°和60°,这时OB绳的拉力大小为F1 , 若烧断O′B绳,当小球运动到最低点C时,OB绳的拉力大小为F2 , 则F1:F2等于( )
A.1:1
B.1:2
C.1:3
D.1:4
【答案】D
【解析】解:烧断水平细线前,小球处于平衡状态,合力为零,
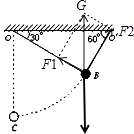
根据几何关系得:F1=mgsin30°= ![]() mg;
mg;
烧断水平细线,设小球摆到最低点时速度为v,绳长为L.小球摆到最低点的过程中,由机械能守恒定律得:
mgL(1﹣sin30°)= ![]() mv2
mv2
在最低点,有 F2﹣mg=m ![]()
联立解得 F2=2mg;
故F1:F2等于1:4;
故选:D.
烧断水平细线前,小球处于平衡状态,合力为零,根据平衡条件求F1.烧断水平细线,当小球摆到最低点时,由机械能守恒定律求出速度,再由牛顿牛顿第二定律求F2.

练习册系列答案
相关题目