题目内容
如图所示，一根长L=1.5m的光滑绝缘细直杆MN，竖直固定在场强为E=1.0×105N/C、与水平方向成θ=30°角的倾斜向上的匀强电场中．杆的下端M固定一个带电小球A，电荷量Q=+4.5×10-6C；另一带电小球B穿在杆上可自由滑动，电荷量q=+1.0×10-6C，质量m=1.0×10-2kg．现将小球B从杆的上端N静止释放，小球B开始运动（静电力常量k=9.0×109N?m2/C2，取g=10m/s2）（1）小球B开始运动时的加速度为多大？
（2）小球B的速度最大时，距M端的高度h1为多大？
分析：对小球B进行受力分析，运用牛顿第二定律求出开始运动时的加速度大小．
根据受力情况分析小球B的运动情况，找出小球B速度最大时的位置特点．
根据受力情况分析小球B的运动情况，找出小球B速度最大时的位置特点．
解答：解：（1）开始运动时小球B受重力、库仑力、杆的弹力和电场力，沿杆方向运动，
由牛顿第二定律得
mg-k
-qEsinθ=ma
代入数据解得a=3.2 m/s2．
（2）小球B向下运动，受A的斥力增大，加速度减小，速度增大，
当小球B速度最大时合力减为零，
即k
+qEsinθ=mg
代入数据解得：h1=0.9m
答：（1）小球B开始运动时的加速度为3.2 m/s2；
（2）小球B的速度最大时，距M端的高度h1为0.9m．
由牛顿第二定律得
mg-k
| L2 |
代入数据解得a=3.2 m/s2．
（2）小球B向下运动，受A的斥力增大，加速度减小，速度增大，
当小球B速度最大时合力减为零，
即k
| h12 |
代入数据解得：h1=0.9m
答：（1）小球B开始运动时的加速度为3.2 m/s2；
（2）小球B的速度最大时，距M端的高度h1为0.9m．
点评：本题要求同学们能够正确对小球B进行受力分析和运动分析，难度适中．
练习册系列答案
相关题目
如图所示，一根长L=0.5m的细绳悬于天花板上O点，绳的另一端挂一个质量为m=1kg的小球，已知绳能承受的最大拉力为12.5N，小球在水平面内做圆周运动，当速度逐渐增大，绳断裂后，小球将平抛后掉在地上．（g=10m/s2）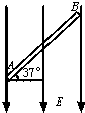
如图所示，一根长L=2m的绝缘细管AB被置于匀强电场E中，其A．B两端正好处于电场的左右边界上，倾角α=37°，电场强度E=103V/m，方向竖直向下，管内有一个带负电的小球，质量m=10-4 kg，电荷量q=2×10-6 C，从A点由静止开始运动，已知小球与管壁的动摩擦因数为5，求：
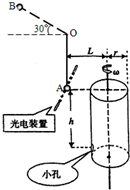如图所示，一根长l=0.8m轻绳一端固定在O点，另一端栓一质量m=0.1kg的小球静止于A点，其右方有底面半径r=0.2m的转筒，转筒顶端与A等高，下部有一小孔，距顶端h=0.8m．现使细绳处于水平线上方30°的位置B点处而伸直，且与转筒的轴线、OA在同一竖直平面内，开始时小孔也在这一竖直平面内．将小球由B点静止释放，当小球经过A点时轻绳突然断掉，同时触动了光电装置，使转筒立刻以某一角速度匀速转动起来，且小球最终正好进入小孔．不计空气阻力，g取l0m/s2．
[物理--选修3-3]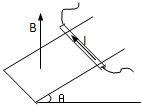
如图所示，一根长L=0.2m的金属棒放在倾角为θ=37°的光滑斜面上，并通以I=5A电流，方向如图所示，整个装置放在磁感应强度为B=0.6T，竖直向上的匀强磁场中，金属棒恰能静止在斜面上，（sin37°=0.6；cos37°=0.8）求：