题目内容
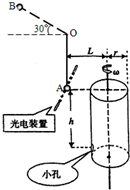 如图所示,一根长l=0.8m轻绳一端固定在O点,另一端栓一质量m=0.1kg的小球静止于A点,其右方有底面半径r=0.2m的转筒,转筒顶端与A等高,下部有一小孔,距顶端h=0.8m.现使细绳处于水平线上方30°的位置B点处而伸直,且与转筒的轴线、OA在同一竖直平面内,开始时小孔也在这一竖直平面内.将小球由B点静止释放,当小球经过A点时轻绳突然断掉,同时触动了光电装置,使转筒立刻以某一角速度匀速转动起来,且小球最终正好进入小孔.不计空气阻力,g取l0m/s2.
如图所示,一根长l=0.8m轻绳一端固定在O点,另一端栓一质量m=0.1kg的小球静止于A点,其右方有底面半径r=0.2m的转筒,转筒顶端与A等高,下部有一小孔,距顶端h=0.8m.现使细绳处于水平线上方30°的位置B点处而伸直,且与转筒的轴线、OA在同一竖直平面内,开始时小孔也在这一竖直平面内.将小球由B点静止释放,当小球经过A点时轻绳突然断掉,同时触动了光电装置,使转筒立刻以某一角速度匀速转动起来,且小球最终正好进入小孔.不计空气阻力,g取l0m/s2.(1)辨析题:求小球到达A点时的速率?
某同学解法如下:小球从B点运动到A点过程中,只有重力做功,故机械能守恒,则mgl(1+sin30°)=
| 1 | 2 |
你认为上述分析是否正确?如果你认为正确,请完成此题;如果你认为不正确,请指出错误,并给出正确的解答.
(2)求转筒轴线距A点的距离L
(3)求转筒转动的角速度ω
分析:(1)此同学解法不正确.由于轻绳突然断掉时,轻绳对小球做功,小球的机械能有损失,不能从B到A过程,运用机械能守恒列方程,解出小球到达A点时的速率.分两段研究:从B到细绳断掉和细绳断掉到A,分别根据机械能定律列式,求解小球到达A点时的速率.细绳断掉过程,小球沿绳子方向的速度突然减至零.
(2)滑块从A点到进入小孔做平抛运动,由高度h求出时间,由几何关系L-r=vA?t求得L.
(3)在小球平抛的时间内,圆桶必须恰好转整数转,小球才能钻入小孔,根据此关系列式,求解转筒转动的角速度ω.
(2)滑块从A点到进入小孔做平抛运动,由高度h求出时间,由几何关系L-r=vA?t求得L.
(3)在小球平抛的时间内,圆桶必须恰好转整数转,小球才能钻入小孔,根据此关系列式,求解转筒转动的角速度ω.
解答: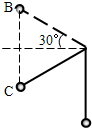 解:(1)此同学解法不正确.设细绳到C位置断掉.
解:(1)此同学解法不正确.设细绳到C位置断掉.
从B→C过程:根据机械能守恒得:mgl=
m
小球在C点切向速度为 vC切=vCsin60°
从C到A,只有重力做功,据机械能守恒定律得
mgl(1-cos60°)+
m
=
m
解得,vA=2
m/s
(2)滑块从A点到进入小孔的时间为
t=
=
s=0.4s
又由题意得 L-r=vA?t
得 L=
m=1.99m
(3)在小球平抛的时间内,圆桶必须恰好转整数转,小球才能钻入小孔
即ωt=2nπ(n=1,2,3…)
解得,ω=5nπ(rad/s)(n=1,2,3…)
答:
(1)此同学解法不正确.小球到达A点时的速率为2
m/s.
(2)转筒轴线距A点的距离L是1.99m
(3)转筒转动的角速度ω是5nπ(rad/s)(n=1,2,3…)
 解:(1)此同学解法不正确.设细绳到C位置断掉.
解:(1)此同学解法不正确.设细绳到C位置断掉.从B→C过程:根据机械能守恒得:mgl=
| 1 |
| 2 |
| v | 2 C |
小球在C点切向速度为 vC切=vCsin60°
从C到A,只有重力做功,据机械能守恒定律得
mgl(1-cos60°)+
| 1 |
| 2 |
| v | 2 C切 |
| 1 |
| 2 |
| v | 2 A |
解得,vA=2
| 5 |
(2)滑块从A点到进入小孔的时间为
t=
|
|
又由题意得 L-r=vA?t
得 L=
4
| ||
| 5 |
(3)在小球平抛的时间内,圆桶必须恰好转整数转,小球才能钻入小孔
即ωt=2nπ(n=1,2,3…)
解得,ω=5nπ(rad/s)(n=1,2,3…)
答:
(1)此同学解法不正确.小球到达A点时的速率为2
| 5 |
(2)转筒轴线距A点的距离L是1.99m
(3)转筒转动的角速度ω是5nπ(rad/s)(n=1,2,3…)
点评:本题是圆周运动与平抛运动相结合的题目,考查了圆周运动及平抛运动的基本规律,运动过程较为复杂,难度较大.

练习册系列答案
相关题目
 如图所示,一根长L=0.5m的细绳悬于天花板上O点,绳的另一端挂一个质量为m=1kg的小球,已知绳能承受的最大拉力为12.5N,小球在水平面内做圆周运动,当速度逐渐增大,绳断裂后,小球将平抛后掉在地上.(g=10m/s2)
如图所示,一根长L=0.5m的细绳悬于天花板上O点,绳的另一端挂一个质量为m=1kg的小球,已知绳能承受的最大拉力为12.5N,小球在水平面内做圆周运动,当速度逐渐增大,绳断裂后,小球将平抛后掉在地上.(g=10m/s2)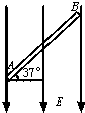 如图所示,一根长L=2m的绝缘细管AB被置于匀强电场E中,其A.B两端正好处于电场的左右边界上,倾角α=37°,电场强度E=103V/m,方向竖直向下,管内有一个带负电的小球,质量m=10-4 kg,电荷量q=2×10-6 C,从A点由静止开始运动,已知小球与管壁的动摩擦因数为5,求:
如图所示,一根长L=2m的绝缘细管AB被置于匀强电场E中,其A.B两端正好处于电场的左右边界上,倾角α=37°,电场强度E=103V/m,方向竖直向下,管内有一个带负电的小球,质量m=10-4 kg,电荷量q=2×10-6 C,从A点由静止开始运动,已知小球与管壁的动摩擦因数为5,求: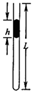 [物理--选修3-3]
[物理--选修3-3]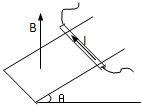 如图所示,一根长L=0.2m的金属棒放在倾角为θ=37°的光滑斜面上,并通以I=5A电流,方向如图所示,整个装置放在磁感应强度为B=0.6T,竖直向上的匀强磁场中,金属棒恰能静止在斜面上,(sin37°=0.6;cos37°=0.8)求:
如图所示,一根长L=0.2m的金属棒放在倾角为θ=37°的光滑斜面上,并通以I=5A电流,方向如图所示,整个装置放在磁感应强度为B=0.6T,竖直向上的匀强磁场中,金属棒恰能静止在斜面上,(sin37°=0.6;cos37°=0.8)求: