题目内容
如图所示，一质量为M的木板静止置于光滑的水平面上，一质量为m的木块以初速度v0滑上木板的左端，已知木块和木板间的动摩擦因素为μ，木块始终没有滑离木板。
（1）求从木块滑上木板开始至二者具有相同的速度所用的时间；
（2）证明从运动开始至二者具有共同速度时，木板对地的位移小于木块对木板的位移。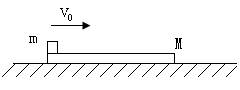
（1）求从木块滑上木板开始至二者具有相同的速度所用的时间；
（2）证明从运动开始至二者具有共同速度时，木板对地的位移小于木块对木板的位移。
（1）
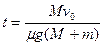（2）证明见解析（1）设二者共同速度大小为V共，木块的加速度大小为a，所求时间为t
以木块和木板为研究对象，其所受合外力为零，由动量守恒定律有：
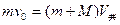① （2分）
木块在摩擦力作用下做匀减速运动，由牛顿第二定律有：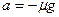
② （1分）
对木块，由匀变速直线运动规律有：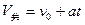
③ （2分）
联立以上三式求解得：
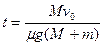， （1分）
（2）设从运动开始到二者具有共同速度时，木块对地的位移为S1，木板对地的位移为S2，木块对木板的位移为
以木块为研究对象，由动能定理有：
④ （3分）
以木板为研究对象，由动能定理有：
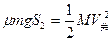⑤ （3分）
又：
⑥ （2分）
联立以上各式求解得：
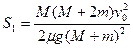
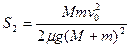
由此可得：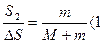
，故证得证结论成立。（2分）
说明：用其它方法计算，只要正确，同样给分。
以木块和木板为研究对象，其所受合外力为零，由动量守恒定律有：
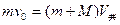① （2分）木块在摩擦力作用下做匀减速运动，由牛顿第二定律有：
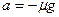② （1分）对木块，由匀变速直线运动规律有：
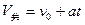③ （2分）联立以上三式求解得：
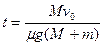， （1分）（2）设从运动开始到二者具有共同速度时，木块对地的位移为S1，木板对地的位移为S2，木块对木板的位移为
以木块为研究对象，由动能定理有：
④ （3分）以木板为研究对象，由动能定理有：
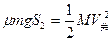⑤ （3分）又：
⑥ （2分）联立以上各式求解得：
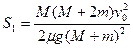
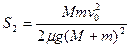
由此可得：
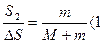，故证得证结论成立。（2分）说明：用其它方法计算，只要正确，同样给分。
练习册系列答案
导学教程高中新课标系列答案
相关题目
取
，不计空气阻力）
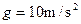，不计空气阻力，结合图像，试求：
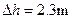，这一过程中蹦床对何雯娜做了多少功？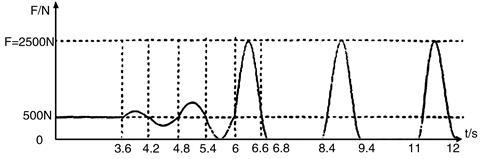
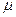，筒与凹槽的滑动摩擦因数为
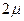，半圆轨道光滑。如图所示，现将两个弹簧的长度均压缩为L/2，且用销钉K将小球和筒固定，发现筒恰好不滑动。现将K突然拔掉，同时对筒施加一方向水平向左的力F，使筒向左匀加速运动，直到筒撞击B处之后使筒立刻停止运动。已知小球的质量为m，筒的质量为2m，设最大静摩擦力等于滑动摩擦力，忽略小球的直径、筒壁和筒底的厚度、筒的内径、外径。
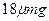，且小球从C处落回后，恰好未撞击筒，求该力在筒撞击B处之前做的功。