题目内容
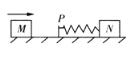
【题目】如图所示，质最相等的两个滑块位于光滑水平桌面上，弹簧两端分别与静止的滑块N和挡板P相连接，弹簧与挡板的质量均不计；滑块M以初速度v0向右运动，它与挡板P碰撞（不粘接）后开始压缩弹簧，最后滑块M与挡板要分开。下列说法正确的是（）
A. 滑块M的速度等于0时，弹簧的弹性势能最大
B. 滑块M与N具有相同的速度时，滑块M与N的动能之和最小
C. 滑块M的速度
时，弹簧的弹性势能最小
D. 滑块M的速度为时，弹簧的弹性势能最大
【答案】BD
【解析】
M与P碰撞压缩弹簧时，M做减速运动，N做加速运动，开始时M的速度大于N的速度，当M与N速度相等时，弹簧被压缩到最短，弹性势能最大，设相等时的速度为v，以M的初速度方向为正方向，根据动量守恒定律得：mv0=2mv，解得：
，故AC错误，D正确；两小球和弹簧的机械能守恒，当弹性势能最大时，两滑块动能之和最小，所以当M与N速度相等时，弹簧被压缩到最短，弹簧弹性势能最大，此时两滑块动能之和最小，故B正确。
练习册系列答案
相关题目
