Question

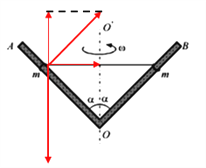
【题目】如图所示，V形细杆AOB能绕其对称轴OO'转动，OO'沿竖直方向，V形杆的两臂与转轴间的夹角均为α=45°。两质量均为m=0.1kg的小环，分别套在V形杆的两臂上，并用长为l=1.2m、能承受最大拉力Fmax=4.5N的轻质细线连结。要求细线始终处于水平伸直状态，取g=10m/s2。则：

(1)若杆光滑，杆转动的角速度的最小值ω0；(结果可以用根式表示)

(2)若杆与球之间的动摩擦因数为0.2，求杆转动的角速度范围。

Answer 1

【答案】(1) (2)

【解析】（1）角速度最小时，环受重力、支持力，二力的合力充当向心力，

在水平方向上有；

在竖直方向上有，其中，联立解得；

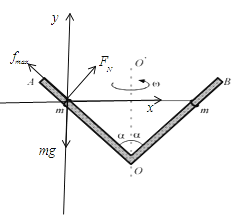
（2）角速度最小时，环受重力、支持力和最大静摩擦力（沿杆向上），

①，②，③

联立解得

当小环有上滑趋势，细线拉力达到最大时，杆转动的角速度最大，最大静摩擦力反向，根据牛顿第二定律，有： ⑤；

⑥，⑦，解得

小球不能相对杆滑动，故角速度取值范围为