Question

（2010?成都二模）足够长的光滑平行金属导轨cd和ef水平放置，在其左端固定一个倾角为θ的光滑金属导轨，导轨相距均为L，在水平导轨和倾斜导轨上，各有一根与导轨垂直的金属杆，两金属杆与水平导轨、倾斜导轨形成一闭合回路．两金属杆质量均为m、电阻均为R，其余电阻不计，杆b被销钉固定在倾斜导轨某处．整个装置处于匀强磁场中，磁感应强度为B，方向竖直向上．当用水平向右、大小F=

3

mg的恒力拉杆a，使其达到最大速度时，立即撤销销钉，发现杆b恰好能在原处仍然保持静止．（重力加速度为g）
（1）求杆a运动中的最大速度v．
（2）求倾斜导轨的倾角θ．
（3）若杆a加速过程中发生的位移为s，则杆a加速过程中，求杆b上产生的热量Q_b．

Answer 1

分析：（1）杆a达到最大速度时，受重力、支持力、拉力和向左的安培力，根据平衡条件求解安培力；根据安培力公式求解电流强度，根据切割公式求解最大速度；
（2）杆b受重力、安培力和支持力，三力平衡，根据平衡条件并运用合成法求解求解斜面倾角；
（3）根据功能关系列式求解电热．

解答：解：（1）对杆a，匀速运动时，拉力与安培力平衡，则F=BIL=

3

mg
得I=

3 mg

BL

杆a产生的电动势E=BLv，回路电流I=

E

2R

，解得：v=

2 3 mgR

B2L2

（2）平衡时，对杆b，受力分析如图所示：

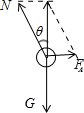
根据平衡条件，有：
BIL=mgtanθ
解得：θ=60°
（3）对杆a的杆b组成的系统，由功能关系，有：
Qa+Qb=FS-

1

2

mv2
其中：Q_a=Q_b
解得：Qb=

3 mgs

2

-

3m3g2R2

B4L4

答：（1）杆a运动中的最大速度v为

2 3 mgR

B2L2

．
（2）倾斜导轨的倾角θ为60°．
（3）杆b上产生的热量Q_b为

3 mgs

2

-

3m3g2R2

B4L4

．

点评：本题关键是力电综合问题，前两问关键受力分析后根据平衡条件列式求解力；第三问关键根据功能关系列式求解．