题目内容
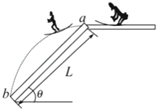
【题目】如图所示，轨道ABO在同一竖直平面内，由光滑水平轨道OB和倾角θ=30°、高度h=1m的倾斜轨道BA连接而成，OB与BA连接处是半径很小的圆弧，水平轨道上一轻质弹簧左端O固定在竖直墙上，质量m=0.5kg的小物块从BA轨道上A点由静止开始下滑，已知物块与倾斜轨道间的动摩擦因数
，重力加速度
，弹簧形变始终在弹性限度内，求：
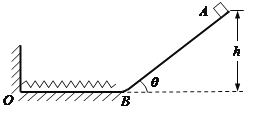
（1）物块在斜面上运动时的加速度大小；
（2）物块第一次在水平轨道上压缩弹簧运动到速度为零时，弹簧具有的弹性势能
；
（3）物块在倾斜轨道上滑动的总路程s；
【答案】（1）2.5m/s2（2）2.5J（3）4m
【解析】（1）由牛顿第二定律可知: 
解得: 
（2）物块从A点到第一次压缩弹簧速度为零过程，由功能关系可得
解得
（3）物块最终静止在水平轨道上，且弹簧形变量为零
由动能定理可得
，
解得
练习册系列答案
相关题目
