题目内容
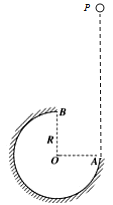
【题目】如图所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时对轨道压力恰好为mg．已知在运动过程中损失的机械能为2mgR，重力加速度为g，不考虑空气阻力，则小球从P到B的运动过程中 ( )
A. AP的距离为3R
B. 重力做功3mgR
C. 合外力做功2mgR
D. 克服摩擦力做功mgR
【答案】B
【解析】
AD.小球沿轨道到达最高点B时对轨道压力为mg,小球受重力和支持力,合力为2mg,向下,根据牛顿第二定律,有:
计算得出:
小球从P到B的过程，根据动能定理可知
由于摩擦力导致机械能损失，所以
解得：
所以AP的距离为4R，故AD错误
B.由于，则小球从P到B的运动过程中重力做功为
，故B正确，
C.根据动能定理可知合外力做功为
，
故C错误
练习册系列答案
阅读快车系列答案
相关题目
