题目内容
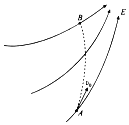
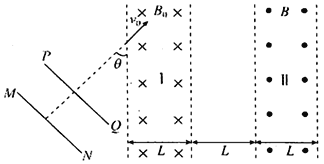
【题目】如图所示,空间有相互平行、相距和宽度也都为L的I、II两区域,I、II区域内有垂直于纸面的匀强磁场,I区域磁场向内、磁感应强度为![]() ,II区域磁场向外,大小待定。现有一质量为
,II区域磁场向外,大小待定。现有一质量为![]() ,电荷量为
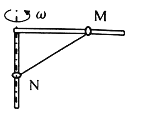
,电荷量为![]() 的带电粒子,从图中所示的一加速电场中的MN板附近由静止释放被加速,粒子经电场加速后平行纸面与I区磁场边界成45°角进入磁场,然后又从I区右边界成45°角射出。
的带电粒子,从图中所示的一加速电场中的MN板附近由静止释放被加速,粒子经电场加速后平行纸面与I区磁场边界成45°角进入磁场,然后又从I区右边界成45°角射出。
(1)求加速电场两极板间电势差![]() ;
;
(2)若II区磁感应强度也是![]() 时,则粒子经过I区的最高点和经过II区的最低点之间的高度差是多少?
时,则粒子经过I区的最高点和经过II区的最低点之间的高度差是多少?
(3)为使粒子能返回I区,II区的磁感应强度![]() 应满足什么条件?并求出粒子从左侧进入I区到从左侧射出I区需要的最长时间。
应满足什么条件?并求出粒子从左侧进入I区到从左侧射出I区需要的最长时间。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,
,![]()
【解析】
(1)画出粒子在磁场中运动的示意图,如图所示:

粒子在加速电场中根据动能定理可得![]()
粒子在I区域做圆周运动,根据洛伦兹力提供向心力可得![]()
根据几何关系可得:![]()
联立可得加速电场两极板间电势差![]()
(2)粒子在II区域运动的半径与I区域相同,
高度差由图中几何关系可得:![]()
可得:![]()
(3)画出粒子刚好从II区域右边界穿出磁场的临界状态,即轨迹圆与右边界相切的情况.
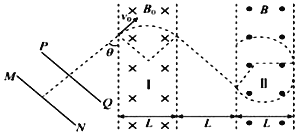
根据几何关系可得![]() ,
,
解得![]()
可知当![]() 时,粒子在II区域中运动的时间最长,即粒子从左侧进入Ⅰ区到从左侧射出Ⅰ区的时间最长
时,粒子在II区域中运动的时间最长,即粒子从左侧进入Ⅰ区到从左侧射出Ⅰ区的时间最长
粒子两次在I区域运动的时间为![]()
粒子两次在磁场之间的时间为![]()
粒子在II区域运动的时间![]()
总时间![]()

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目