题目内容
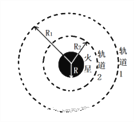
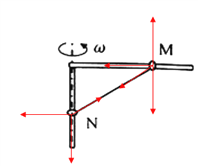
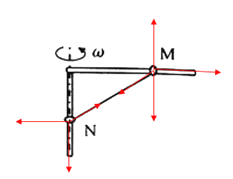
【题目】如图所示，金属环M、N用不可伸长的细线连接，分别套在水平粗糙细杆和竖直光滑细杆上，当整个装置以竖直杆为轴以不同大小的角速度匀速转动时，两金属环一直相对杆不动，下列判断正确的是
A. 转动的角速度越大，细线中的拉力越大
B. 转动的角速度越大，环M与水平杆之间的弹力越大
C. 转动的角速度越大，环N与竖直杆之问的弹力越大
D. 转动的角速度不同，环M与水平杆之间的摩擦力大小可能相等
【答案】D
【解析】试题分析：由于两环相对杆的位置恒定，所以以N为突破口（因为N处于静止状态），对N分析判断细线的拉力以及竖直杆对N作用力的变化；然后对M受力分析，其向心力来源为细线沿水平方向上的分力与摩擦力的合力，随着角速度的变化，摩擦力大小和方向都在变化，据此分析．
设细线与竖直方向的夹角为
，对N受力分析，受到竖直向下的重力
，绳子的拉力T，杆给的水平支持力
，因为两环相对杆的位置不变，所以对N来说处于静止状态，合力为零，故在竖直方向上
，在水平方向上
，因为重力恒定，角度恒定，所以细线的拉力不变，环N与杆之间的弹力恒定，AC错误；对M受力分析，受到绳子的拉力T，竖直向下的重力
，竖直向上的支持力
，以及水平杆给的摩擦力f，在竖直方向上有
，恒定不变，若以较小角速度转动时，摩擦力方向右，即
，随着角速度的增大，摩擦力方向可能变成向左，即
，故可能存在
，摩擦力向左和向右时相等的情况，B错误D正确．
练习册系列答案
阅读快车系列答案
相关题目
