题目内容
(18分)
如图所示,AB、CD均为半径为R的1/4光滑圆弧轨道,BC、DF水平。质量为m可视为质点的物体从A由点静止释放,沿AB下滑,已知BC长L=2R,与两个圆弧相切,物体和BC之间的动摩擦因数为μ=0.25试求:
(1)物体滑到AB圆弧最低点B时轨道对它的支持力N
(2)物体到达C点时的速度大小
(3)物体第一次落在DF段上的E点,求DE的距离s
(1)N=3mg
(2)vc= (gR)1/2
(3)s=0.41R
解析:
(1)A到B:由机械能守恒定律:mgR=mvB2/2 2分
在B点:根据牛顿第二定律有: N-mg=mvB2/R 2分
解得:N=3mg 2分
(2)B到C:由动能定理:-μmgL=mvc2/2-mvB2/2 4分
解得:vc=(gR)1/2 2分
(3)在C点,设轨道对物体的支持力为F,根据牛顿第二定律有
mg-F=mvc2/R 1分 解得F=0 故物体做平抛运动。 1分
由平抛运动规律:R=gt2/2 1分 R+S=vct 1分
解得:s=0.41R 2分

练习册系列答案
相关题目
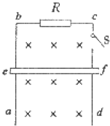 如图所示,ab、cd是固定在竖直平面内的足够长的金属框架,bc段接有一阻值为R的电阻,其余电阻不计,ef是一条不计电阻的金属杆,杆两端与ab和cd接触良好且能无摩擦下滑(不计空气阻力),下滑时ef始终处于水平位置,整个装置处于方向垂直框面向里的匀强磁场中,ef从静止下滑,经过一段时间后闭合开关S,则在闭合开关S后( )
如图所示,ab、cd是固定在竖直平面内的足够长的金属框架,bc段接有一阻值为R的电阻,其余电阻不计,ef是一条不计电阻的金属杆,杆两端与ab和cd接触良好且能无摩擦下滑(不计空气阻力),下滑时ef始终处于水平位置,整个装置处于方向垂直框面向里的匀强磁场中,ef从静止下滑,经过一段时间后闭合开关S,则在闭合开关S后( )| A、ef的加速度大小不可能大于g | B、无论何时闭合开关S,ef最终匀速运动时速度都相同 | C、无论何时闭合开关S,ef最终匀速运动时电流的功率都相同 | D、ef匀速下滑时,减少的机械能大于电路消耗的电能 |
 如图所示,AB和CD是足够长的平行光滑导轨,其间距为L,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,.AC端连有电阻值为R的电阻.若将一质量为M、电阻为r的金属棒EF垂直于导轨在距BD端s处由静止释放,在棒EF滑至底端前会有加速和匀速两个运动阶段.今用大小为F,方向沿斜面向上的恒力把棒EF从BD位置由静止推至距BD端s处,突然撤去恒力F,棒EF最后又回到BD端.(导轨的电阻不计)
如图所示,AB和CD是足够长的平行光滑导轨,其间距为L,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中,.AC端连有电阻值为R的电阻.若将一质量为M、电阻为r的金属棒EF垂直于导轨在距BD端s处由静止释放,在棒EF滑至底端前会有加速和匀速两个运动阶段.今用大小为F,方向沿斜面向上的恒力把棒EF从BD位置由静止推至距BD端s处,突然撤去恒力F,棒EF最后又回到BD端.(导轨的电阻不计) 如图所示,ab、cd是竖直面内两根固定的光滑细杆,ab、cd两端位于相切的两个竖直圆周上,每根杆上都套着一个小滑环(图中未画出),两个滑环分别从a、c处释放(初速为0),用t1、t2依次表示滑环从a到b和从c到d所用的时间,则t1
如图所示,ab、cd是竖直面内两根固定的光滑细杆,ab、cd两端位于相切的两个竖直圆周上,每根杆上都套着一个小滑环(图中未画出),两个滑环分别从a、c处释放(初速为0),用t1、t2依次表示滑环从a到b和从c到d所用的时间,则t1 如图所示,AB和CD为半径为R=1m的1/4圆弧形光滑轨道,BC为一段长2m的水平轨道.质量为2kg的物体从轨道A端由静止释放,若物体与水平轨道BC间的动摩擦因数为0.1,试求:
如图所示,AB和CD为半径为R=1m的1/4圆弧形光滑轨道,BC为一段长2m的水平轨道.质量为2kg的物体从轨道A端由静止释放,若物体与水平轨道BC间的动摩擦因数为0.1,试求: (2012?自贡模拟)如图所示,ab、cd为水平放置的足够长的平行光滑导轨,导轨间距l为0.5m,导轨左端连接一个4Ω的电阻R,将一根质量为0.2kg的金属棒ef垂直地放置导轨上,且与导轨接触良好.金属棒的电阻r大小为1Ω,导轨的电
(2012?自贡模拟)如图所示,ab、cd为水平放置的足够长的平行光滑导轨,导轨间距l为0.5m,导轨左端连接一个4Ω的电阻R,将一根质量为0.2kg的金属棒ef垂直地放置导轨上,且与导轨接触良好.金属棒的电阻r大小为1Ω,导轨的电