��Ŀ����
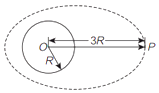
����Ŀ����ͼ��ʾ��B������Ϊ2m���뾶ΪR�Ĺ⻬��Բ���ۣ����ڹ⻬��ˮƽ�����ϣ�A������Ϊ3m��ϸ��ֱ�ˣ��ڹ⻬���������£�Aֻ�������˶������C������Ϊm������B���ã���ʼʱ��A�˱���ס��ʹ���¶��������Բ�����ڲ���ϱ�Ե�Ӵ���Ȼ��Ӿ�ֹ�ͷ�A����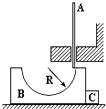
��1����A���¶��˶�����B����͵�ʱB��C���ٶȣ�
��2����A���¶˾�����B����͵��A�����������߶ȣ�
���𰸡�
��1��
�⣺��͵�ʱ����ֱ������ֱ������ٶ�Ϊ0��BC���й�ͬ�ٶ�v���ɣ�����ϵͳABC����е���غ㶨���У�
3mgR= ![]() ��3mv2��
��3mv2��
������v=vB=vC= ![]()
��2��
�⣺B��C��������������ܴﵽ����ߵ�ʱ��AB���ٶȾ�Ϊ0��ABϵͳ��е���غ㣬�У�
![]() ��2mv2=3mgR
��2mv2=3mgR
��ã�h= ![]() R
R
����������1����ֱ�˵��¶˵�һ���˶������ڵ���͵�ʱvB=vC �� �ɻ�е���غ㼴����⣻��2����ֱ�˵��¶�����������ߵ�ʱ��ֱ�����ٶ�Ϊ�㣬���ݻ�е���غ㶨�ɼ�����⣻
�����㾫�������ջ�е���غ㼰�������ǽ����ĸ�������Ҫ֪����ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ��䣮

��ϰ��ϵ�д�
 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ