��Ŀ����
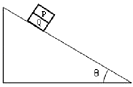
����Ŀ����ͼ��ʾ������Ǧ�=30�㣬���L=1m�Ĺ⻬����϶�����һ����R=9��������������ڴ�ֱ�������ĴŸ�Ӧǿ��B=1T����ǿ�ų��У����ڹ�����ɾ�ֹ�ͷ�һ����m=100g������r=l���Ľ������������»�s=5mʱǡ�ôﵽ����ٶȣ����Ƶ�����裮��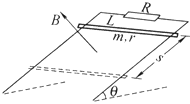
��1�����»�������ٶȣ�
��2�����»����ٶ�Ϊ3m/sʱ���ļ��ٶȴ�СΪ����
��3������R��������������������
���𰸡�
��1��
�⣺�������»��������ٶ����ʱ�����ٶ�a=0������ƽ�������У�
mgsin��=F����
��F��=BIL��I= ![]() ��E=BLvm����ã�F��=
��E=BLvm����ã�F��= ![]()
�ɴ˿ɽ������ٶȣ�vm= ![]()
�������ݽ�ã�vm= ![]() m/s=5m/s
m/s=5m/s
��2��
�⣺����ţ�ٵڶ����ɵã�mgsin�ȩ� ![]() =ma
=ma
��ã�a=gsin�ȩ� ![]()
�������ݵã�a=[10�� ![]() ��
�� ![]() ]m/s2=2m/s2
]m/s2=2m/s2
��3��
�⣺�ɹ��ܹ�ϵ�ɵð����»������в���������Ϊ��
Q=mgssin�ȩ� ![]() mvm2=��0.1��10��5��
mvm2=��0.1��10��5�� ![]() ��
�� ![]() ��J=1.25J��
��J=1.25J��
����R������������������ QR= ![]() Q=
Q= ![]() 1.25J=1.125J
1.25J=1.125J
����������1������������ʼ�˶�ʱ�����ܵ��ع�����ϵİ��������ٶ�����ʱ���������������������ٶ���С�ļ����˶��������ٶȼ�С��0ʱ���ٶȴﵽ��ﵽ�ȶ�״̬�����ݷ����ڵ�Ÿ�Ӧ���ɡ�ŷķ�����Ƶ������������ٶȵĹ�ϵʽ���г�ƽ�ⷽ�̣��������ٶȣ���2�����ݰ������ı���ʽ�������ʱ�İ�����������ţ�ٵڶ����������ٶȴ�С����3���������ص����»�����Ϊs�Ĺ����У��������ܼ�С���������ӣ��������ӣ����������غ����������·������������
�����㾫�������ý������ɶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪��������:Q=I2Rt��ʽ��Q��ʾ����ͨ�������������������λ��J.�������������ǶԴ������·���ǶԷǴ������·�������õģ�