题目内容
(2009?南汇区二模)重力势能EP=mgh实际上是万有引力势能在地面附近的近似表达式,其更精确的表达式应为EP=-G
.式中的G为万有引力恒量,M为地球质量,m为物体的质量,r为物体到地心的距离,并以无限远处的引力势能为零势能.一颗质量为m的地球卫星,在离地高度为H处环绕地球做匀速圆周运动.已知地球的半径为R,地球表面的重力加速度为g,地球质量未知.
试求:
(1)卫星做匀速圆周运动的线速度;
(2)卫星的引力势能;
(3)卫星的机械能;
(4)若要使卫星能飞离地球(飞到引力势能为零的地方),则卫星至少要具有多大的初速度从地面发射?
| Mm | r |
试求:
(1)卫星做匀速圆周运动的线速度;
(2)卫星的引力势能;
(3)卫星的机械能;
(4)若要使卫星能飞离地球(飞到引力势能为零的地方),则卫星至少要具有多大的初速度从地面发射?
分析:(1)卫星在离地高度为H处环绕地球做匀速圆周运动,据万有引力提供向心力,列出等式,根据根据在地面附近物体受到地球的万有引力近似等于物体在地面上的重力,列出等式,两等式结合求解.
(2)根据万有引力势能的表达式求解.
(3)卫星的机械能应该是动能和势能之和.
(4)根据能量守恒,要使卫星能飞离地球,动能转化为引力势能进行求解.
(2)根据万有引力势能的表达式求解.
(3)卫星的机械能应该是动能和势能之和.
(4)根据能量守恒,要使卫星能飞离地球,动能转化为引力势能进行求解.
解答:解:(1)卫星在离地高度为H处环绕地球做匀速圆周运动,据万有引力提供向心力,列出等式:
=
…①
根据根据在地面附近物体受到地球的万有引力近似等于物体在地面上的重力,列出等式:
=mg…②
由①②得:v=R
(2)万有引力势能的表达式:EP=-G
…③
由②③得:卫星的引力势能:EP=-
(3)卫星的机械能应该是动能和势能之和.
所以E=Ek+Ep=-
(4)根据能量守恒,要使卫星能飞离地球,动能转化为引力势能,卫星在地面的引力势能是-G
,要飞到引力势能为零的地方,所以有:
m
-G
=0
得:v0=
答:(1)卫星做匀速圆周运动的线速度是R
;
(2)卫星的引力势能是-
;
(3)卫星的机械能是-
;
(4)若要使卫星能飞离地球(飞到引力势能为零的地方),则卫星至少要具有的初速度是
.
| GMm |
| (R+H)2 |
| mv2 |
| R+H |
根据根据在地面附近物体受到地球的万有引力近似等于物体在地面上的重力,列出等式:
| GMm |
| R2 |
由①②得:v=R
|
(2)万有引力势能的表达式:EP=-G
| Mm |
| r |
由②③得:卫星的引力势能:EP=-
| mgR2 |
| R+H |
(3)卫星的机械能应该是动能和势能之和.
所以E=Ek+Ep=-
| mgR2 |
| 2(R+H) |
(4)根据能量守恒,要使卫星能飞离地球,动能转化为引力势能,卫星在地面的引力势能是-G
| Mm |
| R |
| 1 |
| 2 |
| v | 2 0 |
| Mm |
| R |
得:v0=
| 2gR |
答:(1)卫星做匀速圆周运动的线速度是R
|
(2)卫星的引力势能是-
| mgR2 |
| R+H |
(3)卫星的机械能是-
| mgR2 |
| 2(R+H) |
(4)若要使卫星能飞离地球(飞到引力势能为零的地方),则卫星至少要具有的初速度是
| 2gR |
点评:向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.
运用黄金代换式GM=gR2求出问题是考试中常见的方法.
本题考查了多个知识点的应用,要能根据求解的问题选择恰当的物理规律求解.
运用黄金代换式GM=gR2求出问题是考试中常见的方法.
本题考查了多个知识点的应用,要能根据求解的问题选择恰当的物理规律求解.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
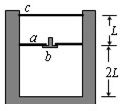 (2009?南汇区二模)如图所示,一个开口向上的圆筒气缸直立于地面上,距缸底2L处固定一个中心开孔的隔板a,在小孔处装有一个能向下开启的单向阀门b,只有当上部压强大于下部压强时,阀门才开启.C为一质量与摩擦均不计的活塞,开始时隔板以下封闭气体压强为1.1P0(P0为大气压强);隔板以上由活塞c封闭的气体压强为P0,活塞c与隔板距离为L.现对活塞c施加一个竖直向下缓慢增大的力F,设气体温度保持不变,已知F增大到Fo时,可产生向下的压强为0.1P0,活塞与隔板厚度均可不计,求:
(2009?南汇区二模)如图所示,一个开口向上的圆筒气缸直立于地面上,距缸底2L处固定一个中心开孔的隔板a,在小孔处装有一个能向下开启的单向阀门b,只有当上部压强大于下部压强时,阀门才开启.C为一质量与摩擦均不计的活塞,开始时隔板以下封闭气体压强为1.1P0(P0为大气压强);隔板以上由活塞c封闭的气体压强为P0,活塞c与隔板距离为L.现对活塞c施加一个竖直向下缓慢增大的力F,设气体温度保持不变,已知F增大到Fo时,可产生向下的压强为0.1P0,活塞与隔板厚度均可不计,求:
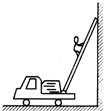 (2009?南汇区二模)如图所示,消防车梯子的下端用光滑铰链固定在车上,上端搁在竖直光滑的墙壁上,当消防队员沿梯子匀速向上爬时,下列说法中正确的是( )
(2009?南汇区二模)如图所示,消防车梯子的下端用光滑铰链固定在车上,上端搁在竖直光滑的墙壁上,当消防队员沿梯子匀速向上爬时,下列说法中正确的是( )