题目内容
2010年 10 月26 日 21时 27 分,北京航天飞行控制中心对“嫦娥二号”卫星实施了降轨控制,卫星成功由轨道半径为 a 、周期为 Tl 的极月圆轨道进入远月点为 A 、周期为T2的椭圆轨道,为在月球虹湾区拍摄图像做好准备,轨道如图所示.则“嫦娥二号”
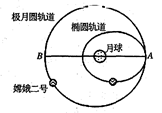
A.在圆轨道运行周期T1小于它在椭圆轨道运行周期T2
B.经过圆轨道上 B 点时的速率等于它经过椭圆轨道上 A 点时的速率
C.在圆轨道上经过 B 点和在椭圆轨道上经过 A 点时的加速度大小相等
D.在圆轨道上经过 B 点和在椭圆轨道上经过 A 点时的机械能相等

A.在圆轨道运行周期T1小于它在椭圆轨道运行周期T2
B.经过圆轨道上 B 点时的速率等于它经过椭圆轨道上 A 点时的速率
C.在圆轨道上经过 B 点和在椭圆轨道上经过 A 点时的加速度大小相等
D.在圆轨道上经过 B 点和在椭圆轨道上经过 A 点时的机械能相等
C
分析:根据开普勒周期定律比较两个轨道上的周期.
当万有引力刚好提供卫星所需向心力时 卫星正好可以做匀速圆周运动
1.若是供大于需 则卫星做逐渐靠近圆心的运动
2.若是供小于需 则卫星做逐渐远离圆心的运动
解答:解:A、根据开普勒周期定律得:
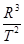 =k,k与中心体有关.
=k,k与中心体有关.由于圆轨道的半径大于椭圆轨道半径,所以在圆轨道运行周期T1大于它在椭圆轨道运行周期T2.故A错误.
B、在椭圆轨道远地点实施变轨成圆轨道是做逐渐远离圆心的运动,要实现这个运动必须万有引力小于所需向心力,所以应给“嫦娥二号”卫星加速,增加所需的向心力,所以经过圆轨道上A点时的速率大于它经过椭圆轨道上A点时的速率,而圆轨道上的各个位置速率相等,故B正确.
C、“嫦娥二号”卫星变轨前通过椭圆轨道远地点时只有万有引力来提供加速度,变轨后沿圆轨道运动也是只有万有引力来提供加速度,所以相等,故C正确.
D、变轨的时候点火,发动机做功,所以“嫦娥二号”卫星点火变轨,前后的机械能不守恒,而圆轨道上的各个位置机械能相等,故D错误.
故答案选C。
点评:卫星变轨也就是近心运动或离心运动,根据提供的万有引力和所需的向心力关系确定.
能够根据圆周运动知识来解决问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目


 ;
; :1 ;
:1 ;  :1。
:1。 的表达式为(k为某个常数)( )
的表达式为(k为某个常数)( ) 员的神舟七号飞船在中国酒泉卫星发射中心发射成功,实现了我国航天技术的又一突破。9月27日瞿志刚成功实施了太空行走,并安全返回神舟七号轨道舱。已知神舟七号飞船在离地球表面h高处的轨道上做圆周运动,地球半径为R,地球表面的重力加速度为g 。
员的神舟七号飞船在中国酒泉卫星发射中心发射成功,实现了我国航天技术的又一突破。9月27日瞿志刚成功实施了太空行走,并安全返回神舟七号轨道舱。已知神舟七号飞船在离地球表面h高处的轨道上做圆周运动,地球半径为R,地球表面的重力加速度为g 。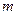 的人造地球卫星,距地面的距离等于地球半径
的人造地球卫星,距地面的距离等于地球半径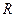 ,已知地面上的重力加速度为
,已知地面上的重力加速度为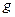 ,求:
,求: