题目内容
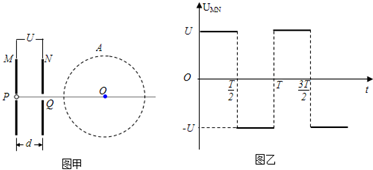
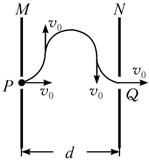
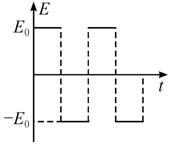
如图甲所示,一对平行放置的金属板M、N的中心各有一小孔P、Q,PQ连线垂直金属板;N板右侧的圆A内分布有方向垂直于纸面向外的匀强磁场,磁感应强度大小为B,圆半径为r,且圆心O在PQ的延长线上.现使置于P处的粒子源连续不断地沿PQ方向放出质量为m、电量为+q的带电粒子(带电粒子的重力和初速度忽略不计,粒子间的相互作用力忽略不计),从某一时刻开始,在板M、N间加上如图乙所示的交变电压,周期为T,电压大小为U.如果只有在每一个周期的0―T/4时间内放出的带电粒子才能从小孔Q中射出,求:

(1)通过计算判断在每一个周期内的哪段时间放出的带电粒子到达Q孔的速度最大.最大速度为多大?
(2)通过计算确定该圆形磁场有带电粒子射出的区域,并在图中标出有带电粒子射出的区域.
答案:
解析:
解析:
|
解:(1)根据题意,在每一个周期内的t=T/4时刻在P处放出的粒子,恰好在t=3T/4时刻到达Q处,且此时速度为0. 设MN间距离为d.在每一个周期内的t=T/4时刻至t=3T/4时刻,则: 设在每一个周期内的0至t时刻放出的带电粒子到达Q孔的速度最大.则每一个周期内的t时刻放出的带电粒子到达Q孔时为T/2时刻.则 由(1)(2)两式得: 在每一个周期内的0至 求得 (2)因为 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目

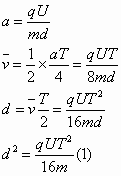

 (2)拉力F作用过程中,电阻R上产生的焦耳热;
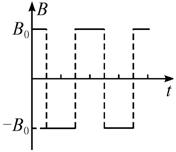
(2)拉力F作用过程中,电阻R上产生的焦耳热; =0.2m,电阻R=1.0Ω;有一导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻均可忽略不计,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直轨道面向下。现用一外力F沿轨道方向向右拉杆,使之做匀加速运动,测得力F与时间t的关系如图乙所示,求杆的质量m和加速度a.
=0.2m,电阻R=1.0Ω;有一导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻均可忽略不计,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直轨道面向下。现用一外力F沿轨道方向向右拉杆,使之做匀加速运动,测得力F与时间t的关系如图乙所示,求杆的质量m和加速度a.