题目内容
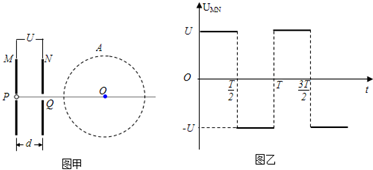
如图甲所示,一对平行放置的金属板M、N的中心各有一小孔P、Q,PQ连线垂直于金属板;N板右侧的圆A内分布有方向垂直于纸面的匀强磁场,磁感应强度大小为B,圆半径为r,且圆心O在PQ的延长线上.现使置于P处的粒子源连续不断地沿PQ方向放出质量为m、电量为q的带电粒子(带电粒子的重力和初速度忽略不计,粒子间的相互作用力忽略不计),从某一时刻开始,在板M、N间加上如图乙所示的交变电压,周期为T,电压大小为U.如果只有在每个周期的0~
时间内放出的带电粒子才能从小孔Q中射出,求:
(1)带电粒子到达Q孔可能的速度范围
(2)带电粒子通过该圆形磁场的最小偏转角θ.
| T | 4 |
(1)带电粒子到达Q孔可能的速度范围
(2)带电粒子通过该圆形磁场的最小偏转角θ.

分析:(1)根据题意分析可知,t=0时刻进入粒子在电场中一直加速,因而根据动能定理,即可求解带电粒子到达Q点的速度范围;
(2)带电粒子在磁场中做圆周运动,由牛顿第二定律,结合向心力公式,即可求出运动的半径,再由速度大,半径大,从而可得出最小偏角.
(2)带电粒子在磁场中做圆周运动,由牛顿第二定律,结合向心力公式,即可求出运动的半径,再由速度大,半径大,从而可得出最小偏角.
解答:解:(1)经分析知,
时刻入射的粒子刚好到Q孔,速度为零,而此时刻进入粒子加速距离为
,则t=0时刻进入粒子加速距离为2d,
所以t=0时刻进入粒子在电场中一直加速,当然射出电场速度最大,设为vm,
则有:qU=
mvm2
解得:vm=
①
带电粒子到达Q点的速度范围为:0≤v≤
①
(2)带电粒子在磁场中做圆周运动,由向心力公式得:qvB=m
,
解得:R=
②
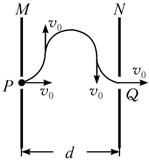
可见,速度大,则半径大,由粒子偏转轨迹图可知,偏转角θ越小.

最大速度vm对应最小偏转角θmin
tan
=
③
联立①②③式解得:θmin=2arctan
答:(1)带电粒子到达Q孔可能的速度范围为:0≤v≤
;
(2)带电粒子通过该圆形磁场的最小偏转角θmin=2arctan
.
| T |
| 4 |
| d |
| 2 |
所以t=0时刻进入粒子在电场中一直加速,当然射出电场速度最大,设为vm,
则有:qU=
| 1 |
| 2 |
解得:vm=
|
带电粒子到达Q点的速度范围为:0≤v≤
|
(2)带电粒子在磁场中做圆周运动,由向心力公式得:qvB=m
| v2 |
| R |
解得:R=
| mv |
| qB |
可见,速度大,则半径大,由粒子偏转轨迹图可知,偏转角θ越小.

最大速度vm对应最小偏转角θmin
tan
| θmin |
| 2 |
| r |
| R |
联立①②③式解得:θmin=2arctan
| Bqr | ||
|
答:(1)带电粒子到达Q孔可能的速度范围为:0≤v≤
|
(2)带电粒子通过该圆形磁场的最小偏转角θmin=2arctan
| Bqr | ||
|
点评:考查动能定理与牛顿第二定律的应用,掌握向心力表达式与运动半径的公式,注意分析得出:当t=0时刻进入粒子在电场中一直加速,同时掌握速度大,则半径大,对应的偏角越小,这是解题的关键之处.

练习册系列答案
相关题目

 (2)拉力F作用过程中,电阻R上产生的焦耳热;
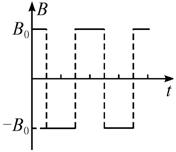
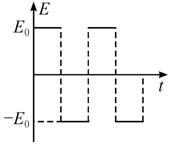
(2)拉力F作用过程中,电阻R上产生的焦耳热; =0.2m,电阻R=1.0Ω;有一导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻均可忽略不计,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直轨道面向下。现用一外力F沿轨道方向向右拉杆,使之做匀加速运动,测得力F与时间t的关系如图乙所示,求杆的质量m和加速度a.
=0.2m,电阻R=1.0Ω;有一导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻均可忽略不计,整个装置处于磁感应强度B=0.5T的匀强磁场中,磁场方向垂直轨道面向下。现用一外力F沿轨道方向向右拉杆,使之做匀加速运动,测得力F与时间t的关系如图乙所示,求杆的质量m和加速度a.