Question

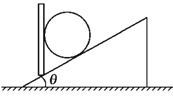
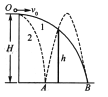
【题目】如图所示为某游乐园滑草场的示意图，某滑道由上下两段倾角不同的斜面组成，斜面倾角θ1>θ2，滑 车与坡面草地之间的动摩擦因数处处相同。载人滑车从坡顶A处由静止开始自由下滑，经过上、下两段滑道后，最后恰好滑到滑道的底端C点停下。若在A、C点位置不变的情况下，将两段滑道的交接点B向左平移一小段距离，使第一段AB的倾角稍稍变大，第二段BC的倾角稍稍变小。不计滑车在两段滑道交接处的机械能损失，则平移后

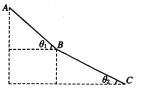
A. 滑车到达滑道底端C点之前就会停下来

B. 滑车仍恰好到达滑道的底端C点停下

C. 滑车到达滑道底端C点后仍具有一定的速度，所以应在C点右侧加安全防护装置

D. 若适当增大滑车与草地之间的动摩擦因数，可使滑车仍恰好到达滑道的底端C点停下

Answer 1

【答案】B

【解析】A、B、C项：对整个过程，由动能定理得：

变形得：，而，其中k为定值即为AC为水平距离，所以滑车到达滑道底端C点的速度与两斜面的角度无关，故A错误，B正确，C错误；

D项：由A、B、C分析可知：，如果增大滑车与草地之间的动摩擦因数，

滑车达滑道底端C点之前就会停下来，故D错误。