题目内容
【题目】如图所示，A、B、C、D是匀强电场中的四个点，它们正好是一个正方形的四个顶点．在A点有一个粒子源，向各个方向发射动能为EK的同种带电粒子，已知到达正方形四个边的粒子中，到B、D两点粒子动能相同，均为2EK不计粒子重力及粒子间相互作用，则（ ）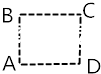
A.电场方向可能由A指向C
B.到达C点粒子动能一定为4EK
C.B，D连线上的各点电势一定相同
D.粒子过AB边中点时，动能一定为 
EK
【答案】A,C,D
【解析】解：A、由题知，粒子从A运动到B与D两点时动能的变化量相等，电场力做功相等，则知B、D两点的电势相等，BD连线是一条等势线，根据电场线与等势面垂直，可知电场方向可能由A指向C，故A正确．
B、对于A到B的过程，由动能定理得
qUAB=2EK﹣EK；
对于A到C的过程，由动能定理得
qUAC=EKC﹣EK；
由于UAC=2UAB，所以解得：到达C点粒子动能 EKC=3EK．故B错误．
C、BD连线是一条等势线，B、D连线上的各点电势一定相同，故C正确．
D、设粒子过AB边中点为F，则对于A到F的过程，由动能定理得
qUAF=EKF﹣EK；
由于UAF= 
UAB，所以解得到达F点的粒子动能为 EKF= 
EK．故D正确．
故选：ACD
【考点精析】掌握动能定理的综合应用是解答本题的根本，需要知道应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．
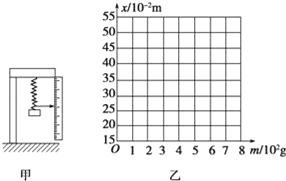
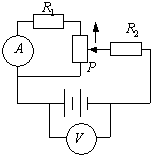
习题精选系列答案
【题目】某同学用如图甲所示装置做探究弹力和弹簧伸长关系的实验．他先测出不挂砝码时弹簧下端指针所指的标尺刻度，然后在弹簧下端挂上砝码，并逐个增加砝码，测出指针所指的标尺刻度，所得数据如表：（重力加速度g取9.8m/s2）
砝码质量m/102g | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.00 |
标尺刻度x/10﹣2m | 15.00 | 18.94 | 22.82 | 26.78 | 30.66 | 34.60 | 42.00 | 54.50 |
（1）根据所测数据，在图乙中作出弹簧指针所指的标尺刻度x与砝码质量m的关系曲线_____．
（2）根据所测得的数据和关系曲线可判断，在_____ N范围内弹力大小与弹簧伸长关系满足胡克定律．这种规格的弹簧劲度系数为_____N/m．
